D2MatE Top
optimize_flex Top

実行例: [tkprog_X_path]/electrical/optimize_mup/optimize_mup.py

注: optimize_mup.pyの機能の一部は、Launcher: ”External applications" => Electrical/Launcher.pyで起動できる 電気特性関連のLauncher.pyのメニューにある、"Hall effect(mu-T fit)" => "mu-T fit (opt_mup)" ダイアログに実装されています。
　以下の説明では、各modeに対応する Launcher:Decay の機能 (ボタン) を Launcher:mu-T fit:[fit] などと書きます。

ルートファイル構成: [tkprog_X_path]/electrical/optimize_mup

以下に典型的な実行環境例を示します

特徴: 多結晶半導体の移動度の温度依存性のフィッティング。移動度モデルは複数の緩和時間 τ をもつ時系列データを指数関数の和でフィッティングする。粒界散乱の指数項と、粒内移動度に分離されるが、粒内移動度の逆数の散乱因子の係数を
線形最小二乗法で解析できるようにしている。

実行ディレクトリ: [tkprog_X_path]/electrical/optimize_mup/test

　入力ファイルのデフォルトは Hall-T.xlsx になっている。
　変更する場合は、起動時引数 --infile=path名 で指定する。

実行例

代表的なmode引数は、--modeが不要。
  1. 既に実行したファイルがある場合は削除する (Launcher:mu-T fit:[clean])
    test> python ..\optimize_mup.py clean
    　ファイルを削除するかどうか聞いてくるので、
    　・ すべて削除する場合は all
    　・ 聞かれているファイル群だけ削除する場合は yes
    　・ 削除しない場合は no
    　を入力し、ENTERを押す
     
  2. 初期化 (Launcher:mu-T fit:[init]): 設定ファイル Hall-T.in、フィッティング変数ファイル Hall-T_parameters.csv を作成
    実行に必要なファイル: Hall-T.xlsx
     　入力データは、Excelファイルのラベル行に "T" がある列を温度データ、"mu" がある列を移動度データとして読み込みます。
    この設定は、--xlalbel, --ylabel引数で変更できます。
    　
    test> python ..\optimize_decay.py init --ntau=5
    initの前段でcleanを実行するため、1と同じことを聞かれるので、all/yes/noを回答する。
    緩和時間の数 ntau を引数で与え、時系列データからτの最大値、最小値を見積もり、緩和時間の対数で均一に分布するように
    τの初期値を決める。
    線形最小二乗法により、係数の初期値を決定する。

    出力例(抜粋):
    Linear variables:
    varname : ['aop', 'a1', 'a2', 'a3', 'a4', 'a5']
    optid : [1, 1, 1, 1, 1, 1]
    fitting parameters: [0, 1, 0, 0, 0, 0]
    constants:
    pi: None 0 0.5 -1.5 1.5 1
    Eb: 0
    s_phi: 0
    Eop: 0.0446

    mlsq_general_optid:
    nvars = 6
    nmatrix = 6
    ai = 0 1 0 0 0 0
    linid = 1 1 1 1 1 1
    matrix index= 0 1 2 3 4 5
    nData = 15
    optimiz_mup.mslq_general3:: Vector and Matrix:
    Si = 0.0006963, 0.008751, 0.000883, 21.29, 2.077e-05, 0.0001181
    Sij= 0.1667, 1.06, 0.06753, 4395, 0.0002878, 0.004369
    1.06, 15, 1.578, 3.353e+04, 0.03928, 0.2188
    0.06753, 1.578, 0.2188, 2341, 0.008414, 0.03928
    4395, 3.353e+04, 2341, 1.216e+08, 15, 175.8
    0.0002878, 0.03928, 0.008414, 15, 0.000501, 0.001996
    0.004369, 0.2188, 0.03928, 175.8, 0.001996, 0.008414
    ai(new)= 0.001209, 0.0006866, -0.00228, -2.752e-08, -0.01668, 0.01073
    ai(org)= 0, 1, 0, 0, 0, 0
    ai_all= 0.001209, 0.0006866, -0.00228, -2.752e-08, -0.01668, 0.01073
    pk= [0, 0, 0.0446, 0, 0, 1, 0.5, 0, -1.5, 0, 1.5, 0, 1, 0]
    ai_all= [0.0012085677536788353, 0.0006865698509415097, -0.0022795435372700013, -2.7519776669288065e-08, -0.01668433517079393, 0.010728535554335394]

    linear fit results:
    varname : aop a1 a2 a3 a4 a5
    ai_new : 0.001209 0.0006866 -0.00228 -2.752e-08 -0.01668 0.01073
    ai_all : 0.001209 0.0006866 -0.00228 -2.752e-08 -0.01668 0.01073
    optid_lin : 1 1 1 1 1 1
    all parameters:
    varname : VB sigma0 Eop aop p1 a1 p2 a2 p3 a3 p4 a4 p5 a5
    fit.pk(org) : 0 0 0.0446 0 0 1 0.5 0 -1.5 0 1.5 0 1 0
    pk_all(new) : 0 0 0.0446 -2.752e-08 0 0.001209 0.5 0.0006866 -1.5 -0.00228 1.5 -2.752e-08 1 -0.01668

    Save configuration parameters to [D:\git\tkProg\tkprog_COE\electrical\optimize_mup\pmodel\Hall-T.in]

    Error in tkfile.open(): [D:\git\tkProg\tkprog_COE\electrical\optimize_mup\pmodel\Hall-T.in] does not exist
    Warning in tkinifile.WriteString: Can not read [D:\git\tkProg\tkprog_COE\electrical\optimize_mup\pmodel\Hall-T.in]
    Save fitting parameters to [D:\git\tkProg\tkprog_COE\electrical\optimize_mup\pmodel\Hall-T_parameters.csv] (save_parameters)
     
    作成されるファイル:

    注: 一部の係数が負になっているが、負の散乱係数は物理的にあり得ない
    　

  3. 入力データの確認 (Launcher:mu-T fit:[plot]): 入力データファイル Hall-T.xlsx を読み込み、プロットする
    test> python ..\optimize_mup.py plot

     
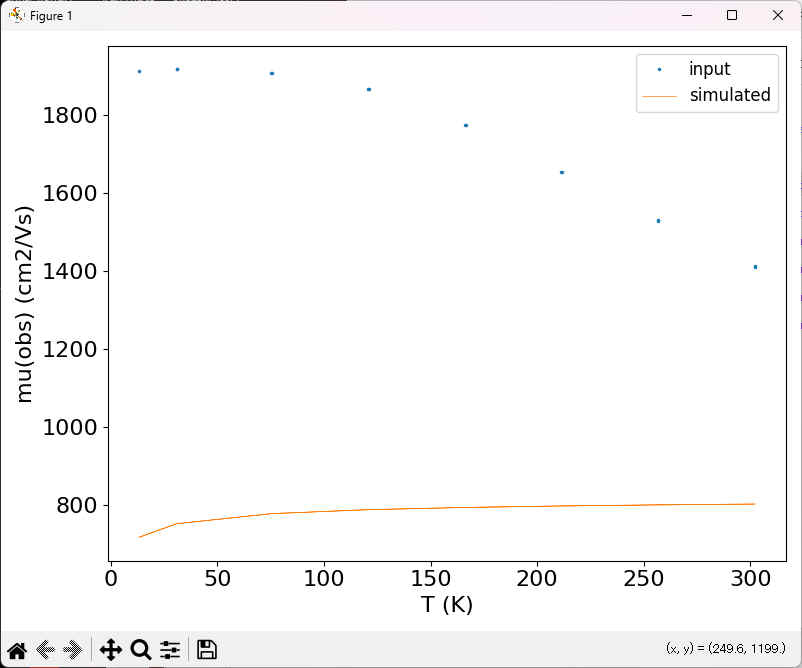
  4. フィッティング変数の初期値の確認 (Launcher:mu-T fit:[sim]): 入力データファイル Hall-T.xlsx とフィッティング変数ファイル Hall-T_parameters.csv を読み込み、入力データとシミュレーション結果をプロットする
    　
    test> python ..\optimize_mup.py sim

     
    注: この場合は、一部の係数が負になっているため、sim、fitモードでは、それらの係数を0として計算する。
    　　そのため、inputとsimulatedに大きな乖離がある
    　
  5. フィッティング (Launcher:mu-T fit:[nl fit for linear params]): 非線形最小二乗法を実行する
    4.のsimでみたようにのように、負の係数のように許容されない値があると、inputとsimulateに大きな違いがある。
    このような場合は、--mode=fitlp により、線形回帰可能な係数 (lined=1) のみで非線形最小二乗法を行います。
    　適当に合ったところで "stop" ボタンを押して最適化を止めます。
    注意: 4.でsimulation結果が良い場合は、直接 6.のfitを行います
    　
    test> python ..\optimize_mup.py fitlp

    　
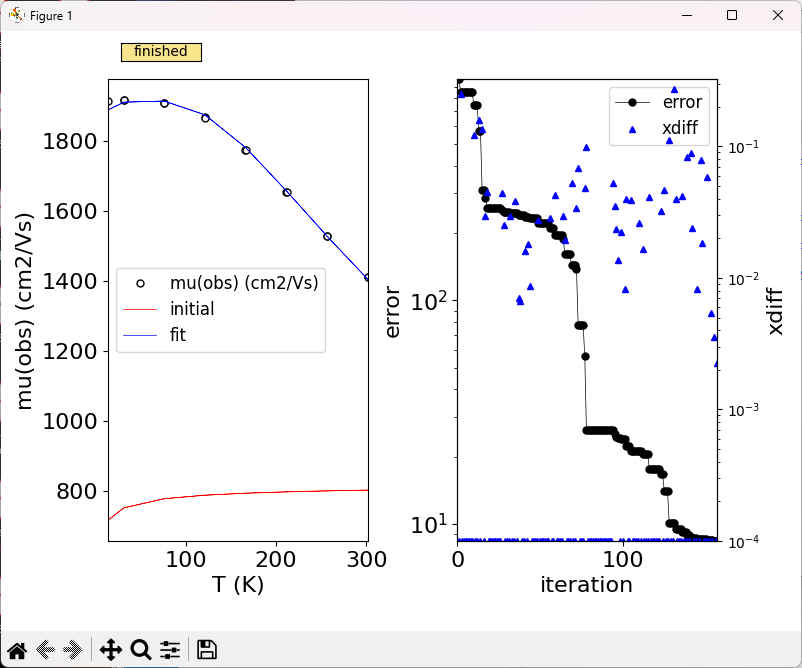
    コンソール出力 (peaks-out.txt):
    Final parameters:
    00: VB= 0 eV (id=1) (linear=0) penality: 1 * (0 - 0.5)
    01: sigma0= 0 eV (id=0) (linear=0) penality: 1 * (0 - 0.5)
    02: Eop= 0.0446 eV (id=0) (linear=0) penality: 1 * (0 - 0.1)
    03: aop= 0.000870352 (id=1) (linear=1) penality: 1 * (0 - 0.01)
    04: p1= 0 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    05: a1= 0.000521097 (id=1) (linear=1) penality: 1 * (0 - 0.01)
    06: p2= 0.5 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    07: a2= 0 (id=1) (linear=1) penality: 1 * (0 - 100)
    08: p3= -1.5 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    09: a3= 0 (id=1) (linear=1) penality: 1 * (0 - 100)
    10: p4= 1.5 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    11: a4= 0.000411432 (id=1) (linear=1) penality: 1 * (0 - 100)
    12: p5= 1 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    13: a5= 0 (id=1) (linear=1) penality: 1 * (0 - 100)
    fmin= 1e+300

    Save configuration parameters to [D:\git\tkProg\tkprog_COE\electrical\optimize_mup\pmodel\Hall-T.in]
    Save fitting parameters to [D:\git\tkProg\tkprog_COE\electrical\optimize_mup\pmodel\Hall-T_parameters.csv] (save_parameters)
    　

  6. フィッティング (Launcher:mu-T fit:[fit]): 全パラメータで非線形最小二乗法を実行する
    test> python ..\optimize_mup.py fit

    　
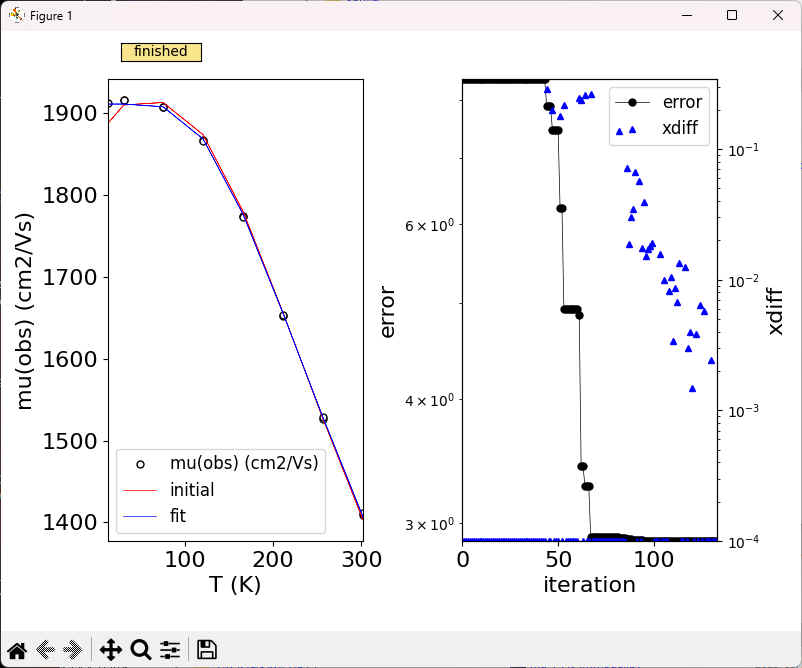
    コンソール出力:
    Final parameters:
    00: VB= 0 eV (id=1) (linear=0) penality: 1 * (0 - 0.5)
    01: sigma0= 0 eV (id=0) (linear=0) penality: 1 * (0 - 0.5)
    02: Eop= 0.0446 eV (id=0) (linear=0) penality: 1 * (0 - 0.1)
    03: aop= 0.00085307 (id=1) (linear=1) penality: 1 * (0 - 0.01)
    04: p1= 0 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    05: a1= 0.000523165 (id=1) (linear=1) penality: 1 * (0 - 0.01)
    06: p2= 0.5 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    07: a2= 0 (id=1) (linear=1) penality: 1 * (0 - 100)
    08: p3= -1.5 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    09: a3= 0 (id=1) (linear=1) penality: 1 * (0 - 100)
    10: p4= 1.5 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    11: a4= 0 (id=1) (linear=1) penality: 1 * (0 - 100)
    12: p5= 1 (id=0) (linear=0) penality: 1 * (-1.5 - 2)
    13: a5= 0 (id=1) (linear=1) penality: 1 * (0 - 100)
    fmin= 2.8778100352882685

    Save configuration parameters to [D:\git\tkProg\tkprog_COE\electrical\optimize_mup\pmodel\Hall-T.in]
    Save fitting parameters to [D:\git\tkProg\tkprog_COE\electrical\optimize_mup\pmodel\Hall-T_parameters.csv] (save_parameters)


    Final data:
    T (K) mu(obs) (cm2/Vs) initial final
    302.3 1409 1403 1406
    256.6 1527 1527 1529
    211.3 1652 1657 1656
    166 1774 1781 1777
    120.7 1867 1874 1869
    75.38 1908 1913 1908
    31.02 1916 1910 1911
    13.28 1913 1888 1911
    30.89 1916 1910 1911
    75.71 1908 1913 1908
    121.2 1866 1874 1868
    166.4 1773 1780 1776
    211.7 1653 1656 1655
    256.9 1529 1527 1528
    302 1411 1404 1407
    Save input, initial, and final data to [mu-fit.xlsx]
     

  7. 十分に収束するまで、フィッティングを繰り返す。
    必要があれば Hall-T_parameters.csv の値 (pk) を修正したり、一部パラメータを固定 (optid=0) したりして
    最適解を求める。
    　

  8. 変数の誤差 (Launcher:mu-T fit:[error]): フィッティングが終了したら、尤度関数を計算し、フィッティング結果の精度を確認する
    test> python ..\optimize_mup.py error 
     

    　
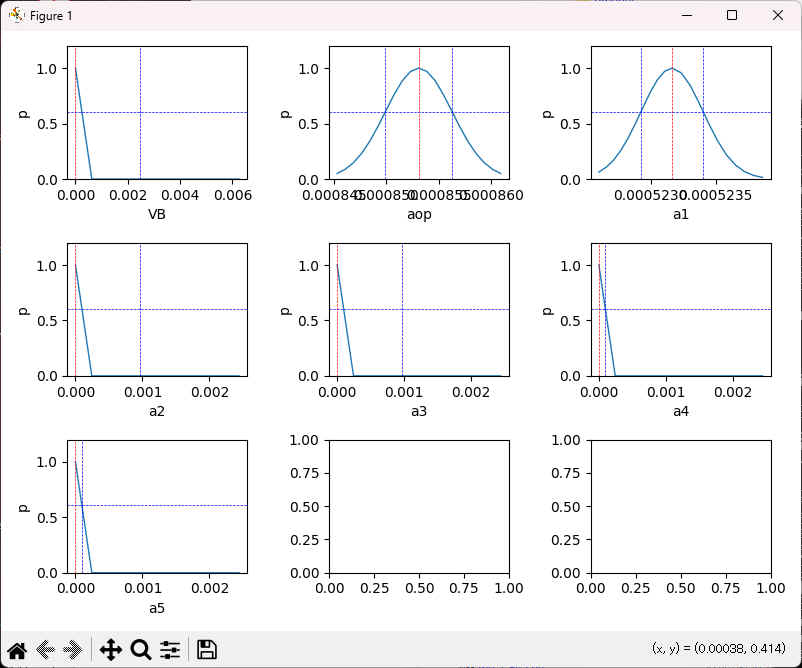
    コンソール出力 (peaks-out.txt):
    Accuracy within one sigma:
    000: VB : 0 * + 0.002459 in ( * - 0.00245918)
    003: aop : 0.00085307 -3.165e-06 + 3.198e-06 in ( 0.000849905 - 0.000856269)
    005: a1 : 0.000523165 -2.392e-07 + 2.394e-07 in ( 0.000522925 - 0.000523404)
    007: a2 : 0 * + 0.0009606 in ( * - 0.000960619)
    009: a3 : 0 * + 0.0009606 in ( * - 0.000960619)
    011: a4 : 0 * + 9.606e-05 in ( * - 9.60619e-05)
    013: a5 : 0 * + 9.606e-05 in ( * - 9.60619e-05)
      
  9. LASSO回帰 (Launcher:mu-T fit:[lasso]): 不要と思われるピークを提案してくれる
    　
    test> python ..\optimize_mup.py lasso

     
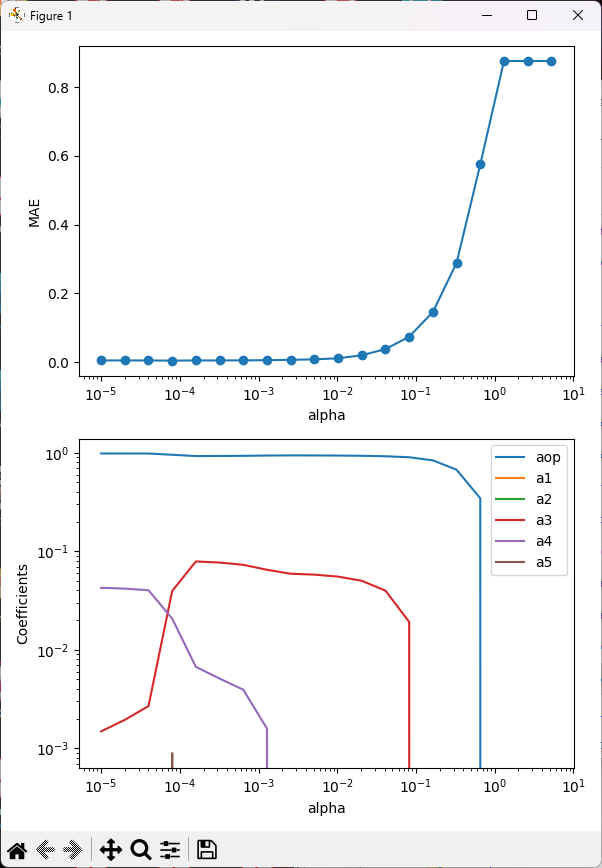
    fit では、a2 ～ a5は0に収束している。LASSO回帰からは、正則化定数αを増やしていくと、a5,a4,a3の順番で係数が０になることがわかる。
    これらが本当に不要かどうかは、これらの係数を 0、optid=0にしてフィッティングし、その結果を見て判断する。
    　
  10. 散乱因子の重み解析
    　
    test> python ..\optimize_mup.py plot weight

     
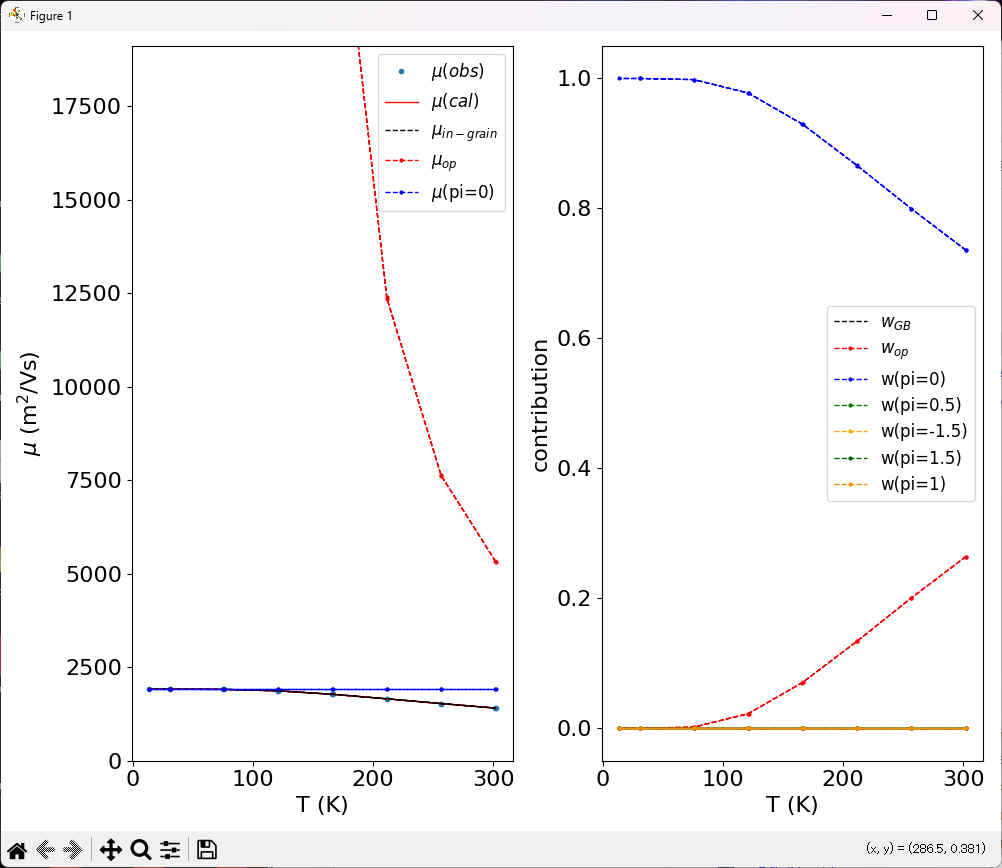
    コンソール出力:
    T(K) KGB mu,op mu(0) mu(0.5) mu(-1.5) mu(1.5) mu(1)
    302 1 5324 1911 1e+10 1e+10 1e+10 1e+10
    257 1 7637 1911 1e+10 1e+10 1e+10 1e+10
    211 1 1.241e+04 1911 1e+10 1e+10 1e+10 1e+10
    166 1 2.534e+04 1911 1e+10 1e+10 1e+10 1e+10
    121 1 8.42e+04 1911 1e+10 1e+10 1e+10 1e+10
    75.4 1 1.123e+06 1911 1e+10 1e+10 1e+10 1e+10
    31 1 1e+10 1911 1e+10 1e+10 1e+10 1e+10
    13.3 1 1e+10 1911 1e+10 1e+10 1e+10 1e+10
    30.9 1 1e+10 1911 1e+10 1e+10 1e+10 1e+10
    75.7 1 1.09e+06 1911 1e+10 1e+10 1e+10 1e+10
    121 1 8.276e+04 1911 1e+10 1e+10 1e+10 1e+10
    166 1 2.51e+04 1911 1e+10 1e+10 1e+10 1e+10
    212 1 1.234e+04 1911 1e+10 1e+10 1e+10 1e+10
    257 1 7620 1911 1e+10 1e+10 1e+10 1e+10
    302 1 5334 1911 1e+10 1e+10 1e+10 1e+10

    T(K) w,gb w,op w(0) w(0.5) w(-1.5) w(1.5) w(1)
    302 0 0.2642 0.7358 1.406e-07 1.406e-07 1.406e-07 1.406e-07
    257 0 0.2002 0.7998 1.529e-07 1.529e-07 1.529e-07 1.529e-07
    211 0 0.1335 0.8665 1.656e-07 1.656e-07 1.656e-07 1.656e-07
    166 0 0.07014 0.9299 1.777e-07 1.777e-07 1.777e-07 1.777e-07
    121 0 0.0222 0.9778 1.869e-07 1.869e-07 1.869e-07 1.869e-07
    75.4 0 0.001699 0.9983 1.908e-07 1.908e-07 1.908e-07 1.908e-07
    31 0 1.911e-07 1 1.911e-07 1.911e-07 1.911e-07 1.911e-07
    13.3 0 1.911e-07 1 1.911e-07 1.911e-07 1.911e-07 1.911e-07
    30.9 0 1.911e-07 1 1.911e-07 1.911e-07 1.911e-07 1.911e-07
    75.7 0 0.00175 0.9982 1.908e-07 1.908e-07 1.908e-07 1.908e-07
    121 0 0.02258 0.9774 1.868e-07 1.868e-07 1.868e-07 1.868e-07
    166 0 0.07075 0.9292 1.776e-07 1.776e-07 1.776e-07 1.776e-07
    212 0 0.1341 0.8659 1.655e-07 1.655e-07 1.655e-07 1.655e-07
    257 0 0.2005 0.7995 1.528e-07 1.528e-07 1.528e-07 1.528e-07
    302 0 0.2638 0.7362 1.407e-07 1.407e-07 1.407e-07 1.407e-07