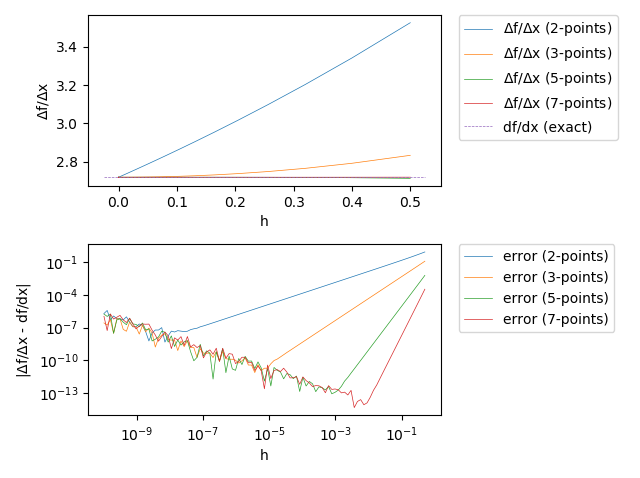
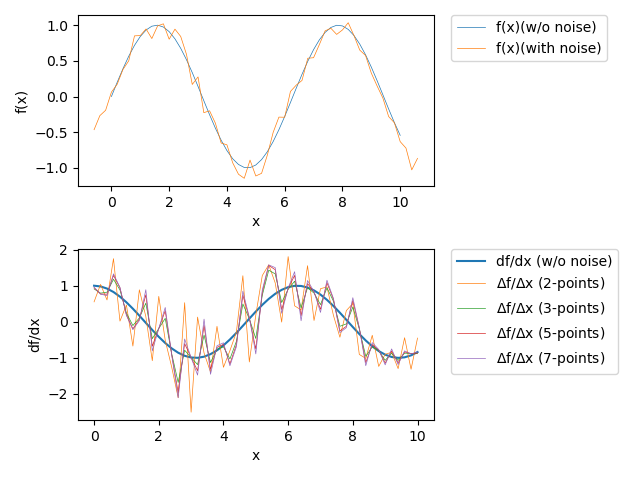
Errors of numerial differentiation for different approxmations
Download script from .\diff_order.py
import csv
import numpy as np
from math import exp
from matplotlib import pyplot as plt
"""
Errors of numerial differentiation for different approxmations
"""
#===================
# parameters
#===================
outfile = 'diff_order.csv'
h = 0.5
kh = 0.8
nh = 101
x0 = 1.0
# define function to be differentiated
def func(x):
return exp(x)
# define analytical deviation of f(x)
def dfdx(x):
return exp(x)
# numerical differentiation by two-point forward difference method
def diff2forward(func, x, h):
return (func(x+h) - func(x)) / h;
def diff2backward(func, x, h):
return (func(x) - func(x-h)) / h;
def diff3(func, x, h):
return (func(x+h) - func(x-h)) / 2.0 / h;
def diff5(func, x, h):
return (-func(x+2.0*h) + 8.0*func(x+h) - 8.0*func(x-h) + func(x-2.0*h)) / 12.0 / h;
def diff7(func, x, h):
return (func(x+3.0*h) - 9.0*func(x+2.0*h) + 45.0*func(x+h)
- 45.0*func(x-h) + 9.0*func(x-2.0*h) - func(x-3.0*h)) / 60.0 / h;
#===================
# main routine
#===================
def main(x0, h, nh):
print("Numerical differentiation using differnet approximations")
print("Write to [{}]".format(outfile))
# open outfile to write a csv file
f = open(outfile, 'w')
fout = csv.writer(f, lineterminator='\n')
fout.writerow([
'Ndiv', 'h',
'Df/Dx(2-point)',
'Df/Dx(3-point)',
'Df/Dx(5-point)',
'Df/Dx(7-point)'
])
fx = func(x0)
f1x = dfdx(x0)
print("")
print("Analytical values:")
print(" f({})={}".format(x0, fx))
print(" df/dx({})={}".format(x0, f1x))
print("{:^3}:\t{:^10}\t"
"{:^16}\t{:^16}\t{:^16}\t{:^16}"
.format(
'Ndiv', 'h',
'Df/Dx(2-point)',
'Df/Dx(3-point)',
'Df/Dx(5-point)',
'Df/Dx(7-point)'
)
)
xh = [h * kh**ih for ih in range(nh)]
ydiff2 = []
ydiff3 = []
ydiff5 = []
ydiff7 = []
errdiff2 = []
errdiff3 = []
errdiff5 = []
errdiff7 = []
for ih in range(nh):
print("{:^3}:\t{:^10.4e}\t".format(ih+1, xh[ih]), end = '')
ydiff2.append(diff2forward(func, x0, xh[ih]))
errdiff2.append(abs(ydiff2[ih] - f1x))
ydiff3.append(diff3(func, x0, xh[ih]))
errdiff3.append(abs(ydiff3[ih] - f1x))
ydiff5.append(diff5(func, x0, xh[ih]))
errdiff5.append(abs(ydiff5[ih] - f1x))
ydiff7.append(diff7(func, x0, xh[ih]))
errdiff7.append(abs(ydiff7[ih] - f1x))
print("{:^16.12f}\t{:^16.12f}\t{:^16.12f}\t{:^16.12f}\t".format(
ydiff2[ih], ydiff3[ih], ydiff5[ih], ydiff7[ih]), end = '')
fout.writerow([ih+1, xh[ih], ydiff2[ih], ydiff3[ih], ydiff5[ih], ydiff7[ih]])
print("")
f.close()
#=============================
# Plot graphs
#=============================
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.plot(xh, ydiff2, label = '$\Delta$f/$\Delta$x (2-points)', linewidth = 0.5)
ax1.plot(xh, ydiff3, label = '$\Delta$f/$\Delta$x (3-points)', linewidth = 0.5)
ax1.plot(xh, ydiff5, label = '$\Delta$f/$\Delta$x (5-points)', linewidth = 0.5)
ax1.plot(xh, ydiff7, label = '$\Delta$f/$\Delta$x (7-points)', linewidth = 0.5)
ax1.plot(ax1.get_xlim(), [f1x, f1x], label = 'df/dx (exact)', linestyle = 'dashed', linewidth = 0.5)
ax1.set_xlabel("h")
ax1.set_ylabel("$\Delta$f/$\Delta$x")
ax1.legend(bbox_to_anchor=(1.05, 1.0), loc='upper left', borderaxespad = 0)
ax2.plot(xh, errdiff2, label = 'error (2-points)', linewidth = 0.5)
ax2.plot(xh, errdiff3, label = 'error (3-points)', linewidth = 0.5)
ax2.plot(xh, errdiff5, label = 'error (5-points)', linewidth = 0.5)
ax2.plot(xh, errdiff7, label = 'error (7-points)', linewidth = 0.5)
ax2.set_xscale('log')
ax2.set_yscale('log')
ax2.set_xlabel("h")
ax2.set_ylabel("|$\Delta$f/$\Delta$x - df/dx|")
ax2.legend(bbox_to_anchor=(1.05, 1.0), loc='upper left', borderaxespad = 0)
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
if __name__ == '__main__':
main(x0, h, nh)