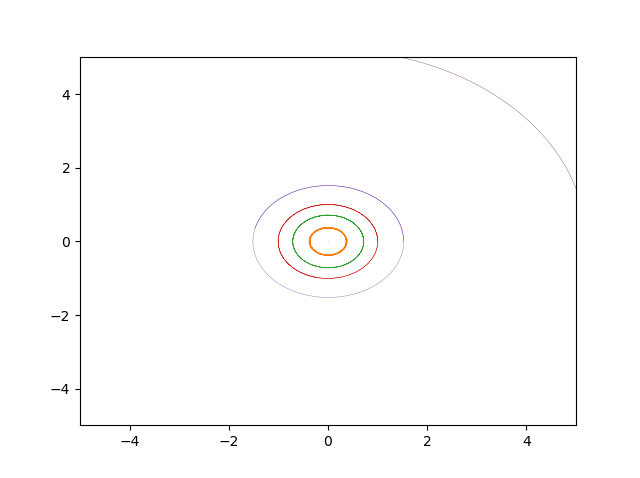
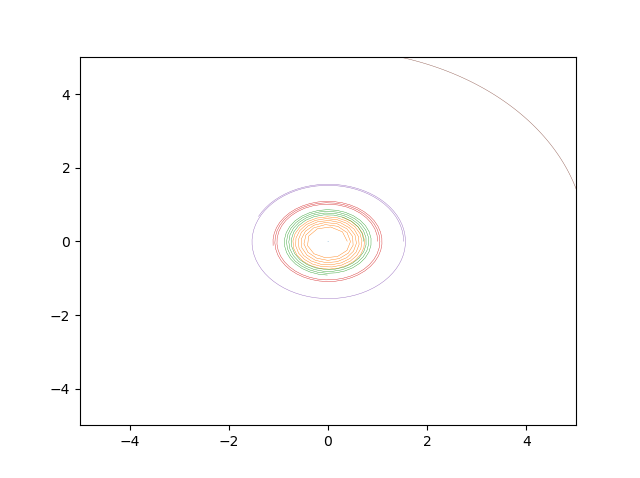
Planet simulator: Solve simulataneous second order diffrential equations
Download script from .\diffeq2nd_planet.py
import sys
import csv
import numpy as np
from math import exp, sqrt, sin, cos, pi
import matplotlib.pyplot as plt
"""
Planet simulator: Solve simulataneous second order diffrential equations
"""
#===================
# constants
#===================
G = 6.67259e-11 #Nm2/kg2
DayToSecond = 60 * 60 * 24 #s
SecondToDay = 1.0 / DayToSecond
AstronomicalUnit = 1.49597870e11 #m
AU = AstronomicalUnit
G1 = G * DayToSecond * DayToSecond / AU / AU / AU
#===================
# parameters
#===================
# algorism to solve differential equations: 'Euler', 'Verlet'
solver = 'Euler'
#solver = 'Verlet'
fplot = 1 # flag to plot graph: 0: not plot, 1: plot
# planet parameter database
dbfile = 'planet_db.csv'
# trajectries of planets
outfile = "diffeq2nd_Planet_{}.csv".format(solver)
# conservation law of total energy (U) and momenta (Px, Py, Pz)
outfile2 = "diffeq2nd_Planet_{}_conservation.csv".format(solver)
# step time to solve diff eq
dt = 0.1
# maximum steps to be calculated
nt = 20000
# display output control
iprint_interval = 100
nprint_planets = 4
# graph output control
iplotdata_interval = 50
iplot_interval = 500
# graph range
xgrange = (-5.0, 5.0)
ygrange = (-5.0, 5.0)
argv = sys.argv
n = len(argv)
if n >= 2:
solver = argv[1]
if n >= 3:
dt = float(argv[2])
if n >= 4:
nt = int(argv[3])
if n >= 5:
fplot = int(argv[4])
#===================
# functions
#===================
def readdb(dbfile):
planets = []
f = open(dbfile, "r");
reader = csv.DictReader(f)
for row in reader:
planets.append(row)
keys = list(planets[0].keys())
for d in planets:
for key in keys:
if key != 'Name':
d[key] = float(d[key])
return planets
def sum(array):
sum = 0.0
for e in array:
sum += e
return sum
def Ptot(it, M, vx, vy, vz):
Px, Py, Pz = 0.0, 0.0, 0.0
Pmsm = 0.0
np = len(M)
for i in range(0, np):
Pxi = M[i] * vx[i][it];
Pyi = M[i] * vy[i][it];
Pzi = M[i] * vz[i][it];
Px += Pxi
Py += Pyi
Pz += Pzi
Pmsm += Pxi*Pxi + Pyi*Pyi + Pzi*Pzi
Pmsm = sqrt(Pmsm / 3.0 / np)
return Px, Py, Pz, Pmsm
# Normalize total momentum to zero
def normalize_momentum(it, M, x, y, z, vx, vy, vz, fx, fy, fz):
Mtot = sum(M)
Px, Py, Pz, Pmsm = Ptot(it, M, vx, vy, vz);
print("Pinitial = {}, {}, {}".format(Px, Py, Pz))
for ip in range(0, len(M)):
vx[ip][it] -= Px / Mtot;
vy[ip][it] -= Py / Mtot;
vz[ip][it] -= Pz / Mtot;
Px, Py, Pz, Pmsm = Ptot(it, M, vx, vy, vz);
print("Pnormalized = {}, {}, {}".format(Px, Py, Pz))
print("")
return Px, Py, Pz
# set initial normalized positions, velocities, forces
def initialize(planets, M, x, y, z, vx, vy, vz, fx, fy, fz):
global AU
global DayToSecond
for i in range(0, len(planets)):
M.append(planets[i]['Mass'])
x.append([planets[i]['Revolution Radius'] / AU])
y.append([0.0])
z.append([0.0])
vx.append([0.0])
vy.append([planets[i]['Revolution Velocity'] * DayToSecond / AU])
vz.append([0.0])
for i in range(0, len(planets)):
fxi, fyi, fzi = Fi(0, i, M, x, y, z)
fx.append([fxi])
fy.append([fyi])
fz.append([fzi])
# total energy
def Utot(istep, M, x, y, z, vx, vy, vz):
U = 0.0
K = 0.0
for i in range(0, len(M)):
K += 0.5 * M[i] \
* (vx[i][istep]*vx[i][istep] + vy[i][istep]*vy[i][istep] + vz[i][istep]*vz[i][istep])
for j in range(i+1, len(M)):
dx = x[j][istep] - x[i][istep]
dy = y[j][istep] - y[i][istep]
dz = z[j][istep] - z[i][istep]
r2 = dx*dx + dy*dy + dz*dz
r = sqrt(r2)
U += G1 * M[i] * M[j] / r
return U, K, U + K
# i - j interplanet normalized force devided by i-th planets mass
def Fij(istep, i, j, M, x, y, z):
dx = x[j][istep] - x[i][istep]
dy = y[j][istep] - y[i][istep]
dz = z[j][istep] - z[i][istep]
r2 = dx*dx + dy*dy + dz*dz
r = sqrt(r2)
g = G1 * M[j]
f = g / r2
fx = f * dx / r
fy = f * dy / r
fz = f * dz / r
return fx, fy, fz
# normalized force on i-th planet devided by its mass
def Fi(istep, i, M, x, y, z):
fxi = 0.0
fyi = 0.0
fzi = 0.0
for j in range(0, len(M)):
if i == j:
continue
fxj, fyj, fzj = Fij(istep, i, j, M, x, y, z)
fxi += fxj
fyi += fyj
fzi += fzj
# print("f={}, {}, {}".format(fxi, fyi, fzi))
return fxi, fyi, fzi
#===================
# main routine
#===================
def main():
global plt
global nt
global dt
print("Planet simulator: Solve simulataneous second order diffrential equations by Euler method")
print("G = {} Nm2/kg2".format(G))
print("AU = {:e} m".format(AU))
print("G1 = {}".format(G1))
print("")
# read planet database
print("Planets:")
planets = readdb(dbfile)
keys = list(planets[0].keys())
for d in planets:
print(" ", d['Name'])
for key in keys:
if key != 'Name':
print(" {}: {}".format(key, d[key]))
print("")
# create list variables and normalize
M = []
x = []
y = []
z = []
xg = []
yg = []
zg = []
vx = []
vy = []
vz = []
fx = []
fy = []
fz = []
initialize(planets, M, x, y, z, vx, vy, vz, fx, fy, fz)
Px, Py, Pz = normalize_momentum(0, M, x, y, z, vx, vy, vz, fx, fy, fz)
print("")
# make label list for display / csv output
labellist = ['t']
for i in range(0, len(planets)):
labellist.append("x({})".format(planets[i]['Name']))
labellist.append("y({})".format(planets[i]['Name']))
# open outfile to write a csv files
print("Write to [{}]".format(outfile))
f = open(outfile, 'w')
fout = csv.writer(f, lineterminator='\n')
fout.writerow(labellist)
f2 = open(outfile2, 'w')
fout2 = csv.writer(f2, lineterminator='\n')
fout2.writerow(['t', 'U', 'K', 'E', 'Px', 'Py', 'Pz', 'Pmsm'])
print("{:^5}".format('t'), end = '')
for i in range(1, nprint_planets*2, 2):
print(" {:^12} {:^12}".format(labellist[i], labellist[i+1]), end = '')
print("")
# create figure object and axes list
if fplot == 1:
fig, ax = plt.subplots(1, 1)
plots = []
# Solve the 1st data by Euler or Heun method
datalist = [0.0]
print("{:^5}".format(0.0), end = '')
for i in range(0, len(planets)):
fx0, fy0, fz0 = Fi(0, i, M, x, y, z)
vx1 = vx[i][0] + dt * fx0
vy1 = vy[i][0] + dt * fy0
vz1 = vz[i][0] + dt * fz0
x1 = x[i][0] + dt * vx[i][0]
y1 = y[i][0] + dt * vy[i][0]
z1 = z[i][0] + dt * vz[i][0]
datalist.append(x[i][0])
datalist.append(y[i][0])
x[i].append(x1)
y[i].append(y1)
z[i].append(z1)
vx[i].append(vx1)
vy[i].append(vy1)
vz[i].append(vz1)
if fplot == 1:
xg.append([x1])
yg.append([y1])
zg.append([z1])
lines, = ax.plot(x[i], y[i], linewidth = 0.3)
plots.append(lines)
for i in range(1, nprint_planets*2, 2):
print(" {:>12.4f} {:>12.4f}".format(x[i][0], y[i][0]), end = '')
print("")
fout.writerow(datalist)
U, K, E = Utot(0, M, x, y, z, vx, vy, vz)
Px, Py, Pz, Pmsm = Ptot(0, M, vx, vy, vz)
fout2.writerow([0.0, U, K, E, Px, Py, Pz, Pmsm])
# Solve the 2nd and later steps
for it in range(1, nt+1):
t = it * dt
# print("it={} t={}".format(it, t))
datalist = [t]
if it % iprint_interval == 0:
print("{:^5}".format(t), end = '')
xmin = 0.0
xmax = 0.0
ymin = 0.0
ymax = 0.0
for i in range(0, len(planets)):
fx0, fy0, fz0 = Fi(it, i, M, x, y, z)
if solver == 'Euler':
vx1 = vx[i][it] + dt * fx0
vy1 = vy[i][it] + dt * fy0
vz1 = vz[i][it] + dt * fz0
x1 = x[i][it] + dt * vx[i][it]
y1 = y[i][it] + dt * vy[i][it]
z1 = z[i][it] + dt * vz[i][it]
elif solver == 'Verlet':
x1 = 2.0 * x[i][it] - x[i][it-1] + dt*dt * fx0
y1 = 2.0 * y[i][it] - y[i][it-1] + dt*dt * fy0
z1 = 2.0 * z[i][it] - z[i][it-1] + dt*dt * fz0
vx1 = (x1 - x[i][it-1]) / 2.0 / dt
vy1 = (y1 - y[i][it-1]) / 2.0 / dt
vz1 = (z1 - z[i][it-1]) / 2.0 / dt
datalist.append(x[i][it])
datalist.append(y[i][it])
x[i].append(x1)
y[i].append(y1)
z[i].append(z1)
vx[i].append(vx1)
vy[i].append(vy1)
vz[i].append(vz1)
if fplot and (it % iplotdata_interval == 0):
xg[i].append(x1)
yg[i].append(y1)
zg[i].append(z1)
# add trajectry data (x[i], y[i]) to the axes object plaots[i]
# get x- and y-ranges to be displayed in the graph
if fplot and i <= 6:
plots[i].set_data(xg[i], yg[i])
xmin = min([xmin] + x[i])
xmax = max([xmax] + x[i])
ymin = min([ymin] + y[i])
ymax = max([ymax] + y[i])
# display output every iprint_interval steps
if it % iprint_interval == 0:
for i in range(1, nprint_planets*2, 2):
print(" {:>12.4g} {:>12.4g}".format(x[i][it], y[i][it]), end = '')
print("")
# write to trajectory csv file
fout.writerow(datalist)
# write to conservation csv file
U, K, E = Utot(it, M, x, y, z, vx, vy, vz)
Px, Py, Pz, Pmsm = Ptot(it, M, vx, vy, vz)
fout2.writerow([t, U, K, E, Px, Py, Pz, Pmsm])
# update the graph every iplot_interval steps
if fplot and it % iplot_interval == 0:
ax.set_xlim(xgrange)
ax.set_ylim(ygrange)
# ax.set_xlim((xmin, xmax))
# ax.set_ylim((ymin, ymax))
plt.pause(0.1)
f.close()
print("Press ENTER to exit>>", end = '')
input()
exit()
if __name__ == '__main__':
main()