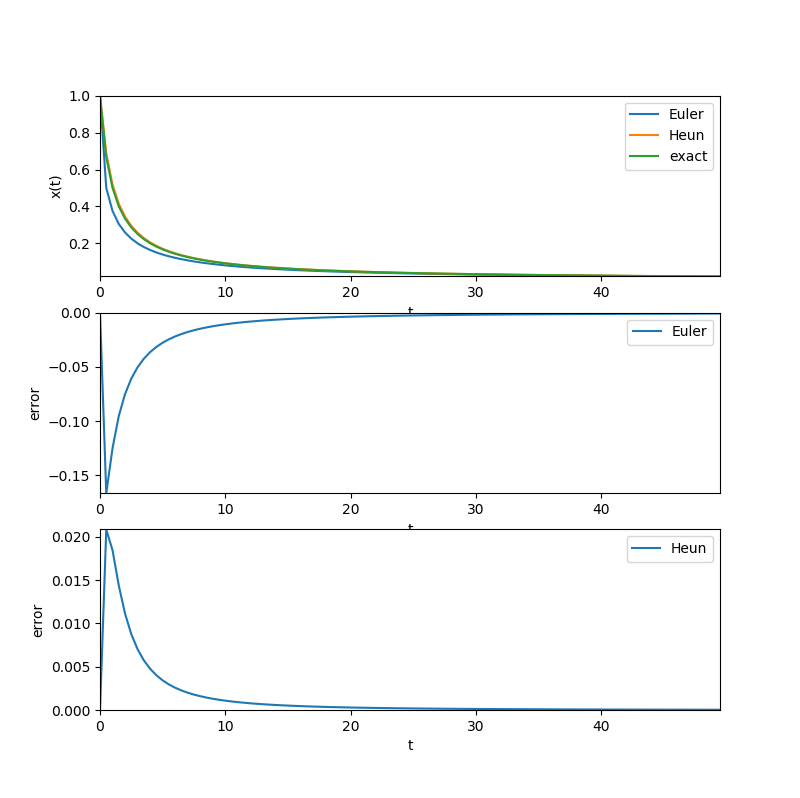
Solve first order diffrential equation by Heun method
Download script from .\diffeq_euler_heun.py
import sys
import csv
import numpy as np
from math import exp, sqrt, sin, cos, pi
import matplotlib.pyplot as plt
"""
Solve first order diffrential equation by Heun method
"""
#===================
# parameters
#===================
outfile = 'diffeq_euler_heun.csv'
x0 = 1.0
dt = 0.1
nt = 501
iprint_interval = 20
argv = sys.argv
n = len(argv)
if n >= 2:
x0 = float(argv[1])
if n >= 3:
dt = float(argv[2])
if n >= 4:
nt = int(argv[3])
if n >= 5:
iprint_interval = int(argv[4])
# dx/dt = dxdt(x,t)
# define function to be integrated
def dxdt(t, x):
return -x*x
# solution: x = 1 / (C + t), C = 1 for x(0) = 1.0
def fsolution(t):
return 1.0 / (1.0 + t)
def diffeq_euler(force, t0, x0, dt):
k1 = dt * dxdt(t0, x0)
x1 = x0 + k1
return x1
def diffeq_heun(force, t0, x0, dt):
k0 = dt * dxdt(t0, x0)
k1 = dt * dxdt(t0+dt, x0+k0)
x1 = x0 + (k0 + k1) / 2.0
return x1
#===================
# main routine
#===================
def main(x0, dt, nt):
print("Solve first order diffrential equation by Heun method")
# prepare for graph
xt = [0.0]
yxex = [x0]
yxeuler = [x0]
yxheun = [x0]
yeeuler = [0.0]
yeheun = [0.0]
fig = plt.figure(figsize = (8, 8))
ax1 = fig.add_subplot(3, 1, 1)
ax2 = fig.add_subplot(3, 1, 2)
ax3 = fig.add_subplot(3, 1, 3)
# 凡例を表示させるため、とりあえずplot()を呼び出す
# 後でプロット毎にデータリストを再設定するので、lineオブジェクトを受け取っておく
line11, = ax1.plot(xt, yxeuler, label = 'Euler')
line12, = ax1.plot(xt, yxheun, label = 'Heun')
line13, = ax1.plot(xt, yxex, label = 'exact')
line21, = ax2.plot(xt, yeeuler, label = 'Euler')
line31, = ax3.plot(xt, yeheun, label = 'Heun')
# ax1.set_xscale('log')
# ax1.set_yscale('log')
ax1.set_xlabel("t")
ax1.set_ylabel("x(t)")
ax1.legend()
ax2.set_xlabel("t")
ax2.set_ylabel("error")
ax2.legend()
ax3.set_xlabel("t")
ax3.set_ylabel("error")
ax3.legend()
# open outfile to write a csv file
f = open(outfile, 'w')
fout = csv.writer(f, lineterminator='\n')
fout.writerow([
't', 'x(cal)', 'x(Euler)', 'x(Heun)'
])
xeuler = x0
xheun = x0
print("{:^5} {:^12} {:^12} {:^12}".format('t', 'x(cal)', 'x(euler)', 'x(heun)'))
for i in range(1, nt):
t0 = i * dt
xeuler = diffeq_euler(force, t0, xeuler, dt)
xheun = diffeq_heun(force, t0, xheun, dt)
xexact = fsolution(t0)
xt.append(t0)
yxex.append(xexact)
yxeuler.append(xeuler)
yxheun.append(xheun)
yeeuler.append(xeuler - xexact)
yeheun.append(xheun - xexact)
# graphをupdateするには、プロットデータ line1/line2 に set_data() でデータリストを設定し、plt.pause()を呼び出す
# set_data() ではグラフの表示範囲は更新されないので、データの最小・最大値で設定する
line11.set_data(xt, yxeuler)
line12.set_data(xt, yxheun)
line13.set_data(xt, yxex)
line21.set_data(xt, yeeuler)
line31.set_data(xt, yeheun)
ax1.set_xlim((min(xt), max(xt)))
ax1.set_ylim((min(yxex), max(yxex)))
ax2.set_xlim((min(xt), max(xt)))
ax2.set_ylim((min(yeeuler), max(yeeuler)))
ax3.set_xlim((min(xt), max(xt)))
ax3.set_ylim((min(yeheun), max(yeheun)))
plt.pause(0.00001)
plt.pause(0.00001)
if i == 1 or i % iprint_interval == 0:
print("t={:5.2f} {:12.6f} {:12.6f} {:12.6f}".format(t0, xexact, xeuler, xheun))
fout.writerow([t0, x0, xeuler, xheun])
f.close()
print("Press ENTER to exit>>", end = '')
input()
exit()
if __name__ == '__main__':
main(x0, dt, nt)