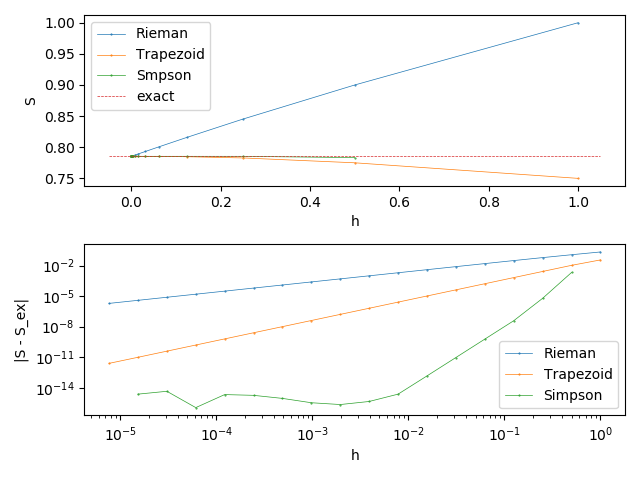
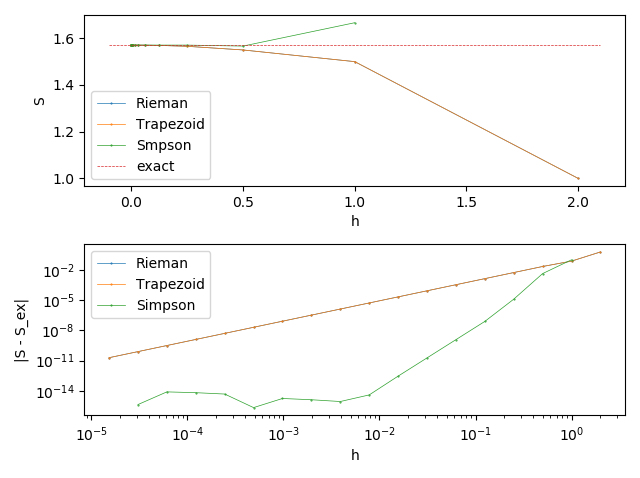
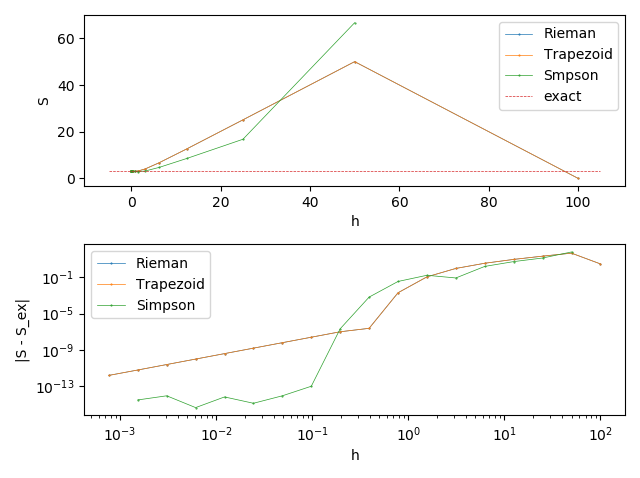
Errors of numerical differentiation for different approxmations
Download script from .\integ_order.py
import csv
import numpy as np
from math import exp
"""
Errors of numerical differentiation for different approxmations
"""
# define function to be differentiated
def func(x):
return exp(x)
# define analytical deviation of f(x)
def integ(x):
return exp(x)
# numerical integration
def integ_rieman(func, x, h):
return func(x) * h
def integ_trapezoid(func, x, h):
return (func(x) + func(x+h)) * 0.5 * h
def integ_simpson(func, x, h):
return (func(x) + 4.0 * func(x+0.5*h) + func(x+h)) / 6.0 * h
def integ_simpson38(func, x, h):
return (3.0*func(x) + 9.0*func(x+h/3.0) + 9.0*func(x+2.0*h/3.0) + 3.0*func(x+h)) / 24.0 * h
def integ_bode(func, x, h):
return (14.0*func(x) + 64.0*func(x+h/4.0) + 24.0*func(x+h/2.0)
+ 64.0*func(x+3.0*h/4.0) + 14.0*func(x+h)) / 180.0 * h
#===================
# parameters
#===================
outfile = 'integ_order.csv'
x0 = 0.0
nx = 10
h = 0.5
#===================
# main routine
#===================
print("Numerical integration using different approximations")
print("Write to [{}]".format(outfile))
# open outfile to write a csv file
f = open(outfile, 'w')
fout = csv.writer(f, lineterminator='\n')
fout.writerow([
'x', 'f', 'integ(f)[x,x+h]',
'Riemtan',
'Trapezoid',
'Simpson',
'Simpson 3/8',
'Bode'
])
print("")
print("{:^3}:\t{:^10}\t{:^10}\t"
"{:^12}\t{:^12}\t{:^12}\t{:^12}\t{:^12}"
.format(
'x', 'f', 'integ(f)[x,x+h]',
'Riemtan',
'Trapezoid',
'Simpson',
'Simpson 3/8',
'Bode'
)
)
for ix in range(nx):
x = x0 + ix * h
fx = func(x)
Fx = integ(x+h) - integ(x)
print("{:^3}:\t{:^10.4f}\t{:^10.4f}\t".format(x, fx, Fx), end = '')
res = []
res.append(integ_rieman(func, x, h))
res.append(integ_trapezoid(func, x, h))
res.append(integ_simpson(func, x, h))
res.append(integ_simpson38(func, x, h))
res.append(integ_bode(func, x, h))
print("{:^12.6f}\t{:^12.6f}\t{:^12.6f}\t{:^12.6f}\t{:^12.6f}\t".format(
res[0], res[1], res[2], res[3], res[4]), end = '')
fout.writerow([x, fx, Fx] + res)
print("")
f.close()