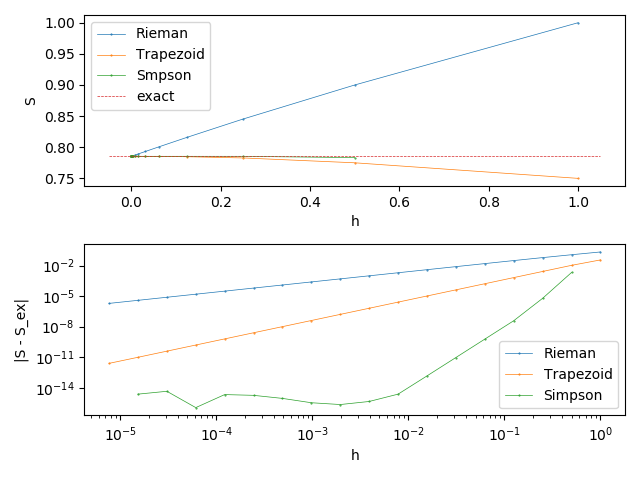
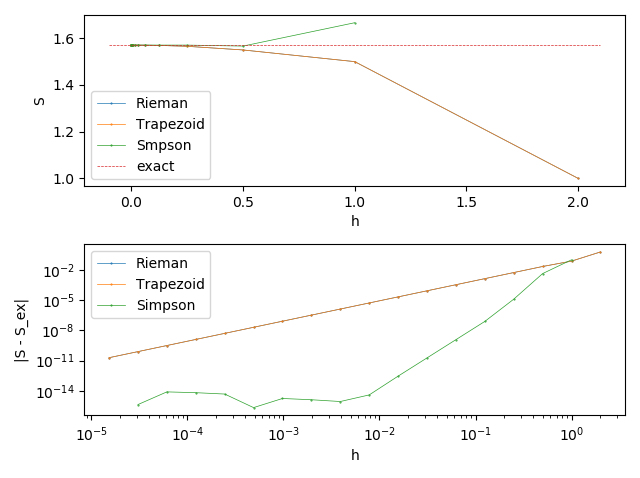
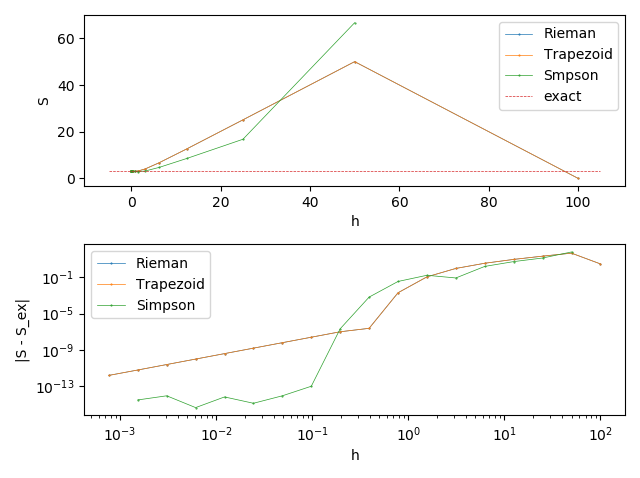
Errors of numerial differentiation for different approxmations and h
Download script from .\integ_order_h.py
import sys
import csv
from math import pi, erf, erfc
import numpy as np
from numpy import sqrt, exp, arctan
from matplotlib import pyplot as plt
"""
Errors of numerial differentiation for different approxmations and h
"""
#===================
# parameters
#===================
xmin = 0.0
xmax = 1.0
nhscan = 18
ftype = None
def usage():
print("")
print("Usage: python {} xmin xmax nhscan func_type".format(argv[0]))
print(" func_type: [lorentz|gauss|exp]")
print(" nhscan: Number of division for the integration range is 2^nhscan (default: 18)")
def terminate():
usage()
print("")
exit()
argv = sys.argv
n = len(argv)
if n >= 2:
xmin = float(argv[1])
if n >= 3:
xmax = float(argv[2])
if n >= 4:
nhscan = int(argv[3])
if n >= 5:
ftype = argv[4]
# define function to be differentiated
def func_Lorentz(x):
return 1.0 / (1 + x * x)
def func_exp(x):
return exp(x)
def func_Gauss(x):
return exp(-x*x)
# define analytical deviation of f(x)
def integ_exact_Lorentz(x):
return arctan(x)
def integ_exact_exp(x):
return exp(x)
def integ_exact_Gauss(x):
return sqrt(pi) / 2.0 * erf(x)
if ftype == 'exp':
func = func_exp
integ_exact = integ_exact_exp
elif ftype == 'gauss':
func = func_Gauss
integ_exact = integ_exact_Gauss
else:
func = func_Lorentz
integ_exact = integ_exact_Lorentz
# numerical integration
def integ_rieman(func, x, h):
return func(x) * h
def integ_trapezoid(func, x, h):
return (func(x) + func(x+h)) / 2.0 * h
def integ_simpson(func, x, h):
return (func(x) + 4.0 * func(x+h) + func(x+2.0*h)) / 6.0 * 2.0 * h
def integ_simpson38(func, x, h):
return (3.0*func(x) + 9.0*func(x+h) + 9.0*func(x+2.0*h) + 3.0*func(x+3.0*h)) / 24.0 * 3.0 * h
def integ_bode(func, x, h):
return (14.0*func(x) + 64.0*func(x+h) + 24.0*func(x+2.0*h)
+ 64.0*func(x+3.0*h) + 14.0*func(x+4.0*h)) / 180.0 * 4.0 * h
#===================
# main routine
#===================
def main():
print("")
print("Numerical integration using different approximations")
print("Function: ", ftype)
print("integration range: {} - {}".format(xmin, xmax))
S_ex = integ_exact(xmax) - integ_exact(xmin)
print(" Exact: {}".format(S_ex))
xrieman = []
yrieman = []
erieman = []
print("")
print("Rieman")
print("{:8}\t{:8}\t{:14}\t{:8}".format('nh', 'h', 'S', 'error'))
for ih in range(nhscan):
nh = int(1 * 2**ih + 0.00001)
h = (xmax - xmin) / nh
nx = int((xmax - xmin) / h + 1.00001)
S = 0.0
for i in range(nx-1):
S += integ_rieman(func, xmin + i * h, h)
xrieman.append(h)
yrieman.append(S)
error = abs(S - S_ex)
erieman.append(error)
print("{:8d}\t{:8.4g}\t{:14.8g}\t{:8.4g}".format(nh, h, S, error))
xtrapezoid = []
ytrapezoid = []
etrapezoid = []
print("")
print("Trapezoid")
print("{:8}\t{:8}\t{:14}\t{:8}".format('nh', 'h', 'S', 'error'))
for ih in range(nhscan):
nh = int(1 * 2**ih + 0.00001)
h = (xmax - xmin) / nh
nx = int((xmax - xmin) / h + 1.00001)
S = 0.0
for i in range(nx-1):
S += integ_trapezoid(func, xmin + i * h, h)
xtrapezoid.append(h)
ytrapezoid.append(S)
error = abs(S - S_ex)
etrapezoid.append(error)
print("{:8d}\t{:8.4g}\t{:14.8g}\t{:8.4g}".format(nh, h, S, error))
xsimpson = []
ysimpson = []
esimpson = []
print("")
print("Simpson")
print("{:8}\t{:8}\t{:14}\t{:8}".format('nh', 'h', 'S', 'error'))
for ih in range(nhscan - 1):
nh = int(2 * 2**ih + 0.00001)
h = (xmax - xmin) / nh
S = 0.0
for i in range(0, nh, 2):
S += integ_simpson(func, xmin + i * h, h)
xsimpson.append(h)
ysimpson.append(S)
error = abs(S - S_ex)
esimpson.append(error)
print("{:8d}\t{:8.4g}\t{:14.8g}\t{:8.4g}".format(nh, h, S, error))
xbode = []
ybode = []
ebode = []
print("")
print("Bode")
print("{:8}\t{:8}\t{:14}\t{:8}".format('nh', 'h', 'S', 'error'))
for ih in range(nhscan - 2):
nh = int(4 * 2**ih + 0.00001)
h = (xmax - xmin) / nh
S = 0.0
for i in range(0, nh, 4):
S += integ_bode(func, xmin + i * h, h)
xbode.append(h)
ybode.append(S)
error = abs(S - S_ex)
ebode.append(error)
print("{:8d}\t{:8.4g}\t{:14.8g}\t{:8.4g}".format(nh, h, S, error))
#=============================
# Plot graphs
#=============================
fig = plt.figure()
ax1 = fig.add_subplot(2, 1, 1)
ax2 = fig.add_subplot(2, 1, 2)
ax1.plot(xrieman, yrieman, label = 'Rieman', linewidth = 0.5, color = 'black', marker ='o', markersize = 1.5)
ax1.plot(xtrapezoid, ytrapezoid, label = 'Trapezoid', linewidth = 0.5, color = 'red', marker ='^', markersize = 1.5)
ax1.plot(xsimpson, ysimpson, label = 'Simpson', linewidth = 0.5, color = 'blue', marker ='v', markersize = 1.5)
ax1.plot(xbode, ybode, label = 'Bode', linewidth = 0.5, color = 'green', marker ='s', markersize = 1.5)
ax1.plot(ax1.get_xlim(), [S_ex, S_ex], label = 'exact', linestyle = 'dashed', linewidth = 0.5)
# ax1.set_xscale('log')
# ax1.set_yscale('log')
ax1.set_xlabel("h")
ax1.set_ylabel("S")
# ax1.legend(bbox_to_anchor=(1.05, 1.0), loc='upper left', borderaxespad = 0)
ax1.legend()
ax2.plot(xrieman, erieman, label = 'Rieman', linewidth = 0.5, color = 'black', marker ='o', markersize = 1.5)
ax2.plot(xtrapezoid, etrapezoid, label = 'Trapezoid', linewidth = 0.5, color = 'red', marker ='^', markersize = 1.5)
ax2.plot(xsimpson, esimpson, label = 'Simpson', linewidth = 0.5, color = 'blue', marker ='v', markersize = 1.5)
ax2.plot(xbode, ebode, label = 'Bode', linewidth = 0.5, color = 'green', marker ='s', markersize = 1.5)
ax2.set_xscale('log')
ax2.set_yscale('log')
ax2.set_xlabel("h")
ax2.set_ylabel("|S - S_ex|")
# ax2.legend(bbox_to_anchor=(1.05, 1.0), loc='upper left', borderaxespad = 0)
ax2.legend()
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
terminate()
if __name__ == '__main__':
main()