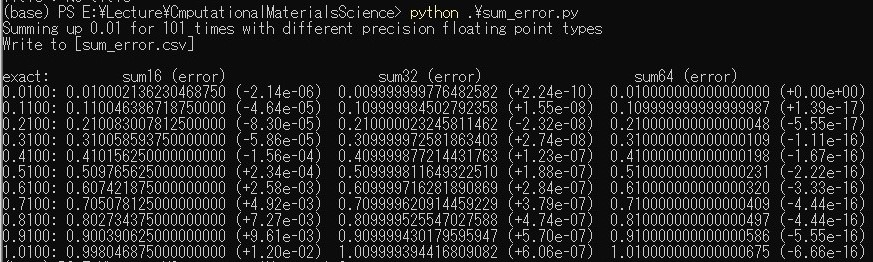
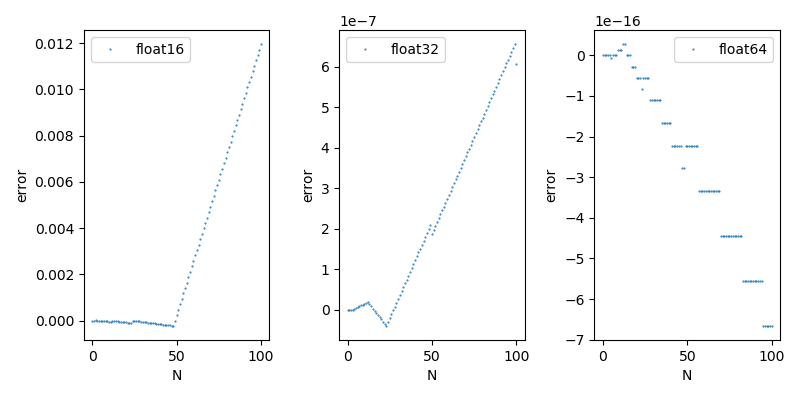
Note: Standard python has only 64bit double precision for floating point type.
Numerical python module (numpy) can handle different precisions for ndarray type
np.float16 # half precision (半精度 浮動小数点数)
np.float32 # single precision (単精度 浮動小数点数)
np.float64 # double precision (倍精度 浮動小数点数)
np.float128 # quadruple (double-double) precision (四倍精度 浮動小数点数)
# numpy for Anaconda ver 3.7 may not support np.float128
Download script from .\sum_error.py
import sys
import csv
import numpy as np
"""
Note: Standard python has only 64bit double precision for floating point type.
Numerical python module (numpy) can handle different precisions for ndarray type
np.float16 # half precision (半精度 浮動小数点数)
np.float32 # single precision (単精度 浮動小数点数)
np.float64 # double precision (倍精度 浮動小数点数)
np.float128 # quadruple (double-double) precision (四倍精度 浮動小数点数)
# numpy for Anaconda ver 3.7 may not support np.float128
"""
#===================
# parameters
#===================
outfile = 'sum_error.csv'
h = 0.01
n = 101
iprintstep = 10
def getintarg(iarg, defval = None):
try:
return int(argv[iarg])
except:
return defval
def getfloatarg(iarg, defval = None):
try:
return float(argv[iarg])
except:
return defval
argv = sys.argv
narg = len(argv)
if narg <= 2:
print("")
print("Usage: python sum_error.py h n iPrintStep")
print(" Summing up h for n times with different precision interger types.")
print(" Output every iPrintStep steps")
print("")
exit()
else:
h = getfloatarg(1, h)
n = getintarg(2, n)
iprintstep = getintarg(3, iprintstep)
#==========================================================
# define precision types as the first elements of ndarrays
# all the variables will be refered to e.g. as h16[0], sum16[0] ...
#==========================================================
h16 = np.array([h], dtype=np.float16)
sum16 = np.array([0.0], dtype=np.float16)
h32 = np.array([h], dtype=np.float32)
sum32 = np.array([0.0], dtype=np.float32)
h64 = np.array([h], dtype=np.float64)
sum64 = np.array([0.0], dtype=np.float64)
#h128 = np.array([h], dtype=np.float128)
#sum128 = np.array([0.0], dtype=np.float128)
# error variables should have the highest precision
ex = np.array([0.0], dtype=np.float64)
err16 = np.array([0.0], dtype=np.float64)
err32 = np.array([0.0], dtype=np.float64)
err64 = np.array([0.0], dtype=np.float64)
#===================
# main routine
#===================
print("")
print("Summing up {} for {} times with "
"different precision floating point types".format(h, n))
print("Write to [{}]".format(outfile))
# open outfile to write a csv file
f = open(outfile, 'w')
fout = csv.writer(f, lineterminator='\n')
fout.writerow(['exact', 'float16', 'float32', 'float64',
'error(float16)', 'error(float32)', 'error(float64'])
print("")
print("{:^3}:\t{:^28}\t{:^28}\t{:^28}".format('exact', 'sum16 (error)', 'sum32 (error)', 'sum64 (error)'))
for i in range(n): # repeat n times from i = 0 to n-1
ex[0] = (i+1) * h
sum16[0] += h16[0]
err16[0] = ex[0] - sum16[0]
sum32[0] += h32[0]
err32[0] = ex[0] - sum32[0]
sum64[0] += h64[0]
err64[0] = ex[0] - sum64[0]
# sum128 += h128
# err128 = ex - sum128[0]
fout.writerow([ex[0], sum16[0], sum32[0], sum64[0], err16[0], err32[0], err64[0]])
if(i % iprintstep == 0):
print("{:<0.4f}: ".format(ex[0]), end = '')
print("{:<0.18f} ({:<+9.2e}) ".format(sum16[0], err16[0]), end = '')
print("{:<0.18f} ({:<+9.2e}) ".format(sum32[0], err32[0]), end = '')
print("{:<0.18f} ({:<+9.2e}) ".format(sum64[0], err64[0]), end = '')
print("")
f.close()
print("")