Bose凝縮の計算
mode = Fs: F_sigma(alpha) 関数の表示
mode = mu: mu (chamical potential), N', n0の計算
Download script from .\bose_condensation.py
import sys
import time
from math import exp, sqrt
import numpy as np
from scipy import integrate # 数値積分関数 integrateを読み込む
from scipy import optimize # newton関数はscipy.optimizeモジュールに入っている
from matplotlib import pyplot as plt
"""
Bose凝縮の計算
mode = Fs: F_sigma(alpha) 関数の表示
mode = mu: mu (chamical potential), N', n0の計算
"""
#定数
pi = 3.14159265358979323846
h = 6.6260755e-34 # Js";
hbar = 1.05459e-34 # "Js";
c = 2.99792458e8 # m/s";
e = 1.60218e-19 # C";
kB = 1.380658e-23 # JK-1";
me = 9.1093897e-31 # kg";
mp = 1.6726231e-27 # kg";
mn = 1.67495e-27 # kg";
zeta32 = 0
# mode = [Fs|mu]
mode = 'Fs' # Fs-α=-mu/kB/Tプロット
#mode = 'mu' # mu-Tプロット
# 有効質量、電子濃度
m = 6.64e-27 # kg, 4He
N = 2.18e22 # cm^-3, Liq He
# Temperature range
Tmin = 3.00 # K
Tmax = 4.00
Tstep = 0.01
# alpha = -EF / kB / T range
alphamin = 0.0
alphamax = 2.0
alphastep = 0.02
#muの誤差がepsより小さくなったら計算終了。TC付近ではEFが10^-9程度にもなるので、小さい値を指定
eps = 1.0e-12
#二分法の最大繰り返し数
nmaxiter = 100
#繰り返し中に途中経過を出力するサイクル数
iprintiterval = 1
# 起動時引数
argv = sys.argv
if len(argv) <= 1:
print("Usage: python bose_condensation.py mu Tmin Tmax Tstep")
print("Usage: python bose_condensation.py Fs Tmin Tmax Tstep alphamin alphamax alphastep")
print(" ex: python bose_condensation.py mu 2.5 4.5 0.01")
print(" ex: python bose_condensation.py Fs 3 4.5 0.2 0 0.5 0.002")
exit()
if len(argv) >= 2:
mode = argv[1]
if len(argv) >= 3:
Tmin = float(argv[2])
if len(argv) >= 4:
Tmax = float(argv[3])
if len(argv) >= 5:
Tstep = float(argv[4])
if len(argv) >= 6:
alphamin = float(argv[5])
if len(argv) >= 7:
alphamax = float(argv[6])
if len(argv) >= 8:
alphastep = float(argv[7])
nT = int((Tmax - Tmin) / Tstep + 1.00001)
nalpha = int((alphamax - alphamin) / alphastep + 1.00001)
# Γ関数
def Gamma(sigma):
if abs(sigma - 1.0) < 1.0e-6:
return 1.0
if abs(sigma - 0.5) < 1.0e-6:
return sqrt(pi)
if sigma < 0.5 - 1.0e-6:
print("Gamma: Abnormal argment sigma = ", sigma)
print(" Exit")
exit()
return (sigma - 1.0) * Gamma(sigma - 1.0)
# Fs(σ, α)の被積分関数
def IntegFunc(y, sigma, alpha):
if y + alpha > 100.0:
return 0.0
return pow(y, sigma - 1.0) / (exp(y + alpha) - 1.0)
# Fs(σ, α)
def Fsalpha(sigma, alpha, Emax = 10.0, eps = 1.0e-8):
ret = integrate.quad(lambda y: IntegFunc(y, sigma, alpha), 0.0, Emax, epsrel = eps)
return 1.0 / Gamma(sigma) * ret[0]
# EFを与えてT>Tcでの電子濃度を求める
def Ne(EF, T, Emax = 10.0, eps = 1.0e-8):
lambdaT = h / sqrt(2.0 * pi * m * kB * T)
alpha = -EF / (kB * T / e)
Ne = 1.0 / pow(lambdaT, 3.0) * Fsalpha(1.5, alpha, Emax = Emax, eps = eps) * 1.0e-6
return Ne
# 二分法でEFを求める
def CalEF(T, N, EFmin, EFmax):
# まず、EFmin,EFmaxにおけるΔQを計算し、それぞれが正・負あるいは負・生となっていることを確認する
dQmin = Ne(EFmin, T) - N
dQmax = Ne(EFmax, T) - N
# print(" EFmin = {:12.8f} dQmin = {:12.4g}".format(EFmin, dQmin))
# print(" EFmax = {:12.8f} dQmax = {:12.4g}".format(EFmax, dQmax))
if dQmin * dQmax > 0.0:
print("Error: Initial Emin and Emax should be chosen as dQmin * dQmax < 0")
return 0
# 二分法開始
for i in range(nmaxiter):
EFhalf = (EFmin + EFmax) / 2.0
dQhalf = Ne(EFhalf, T) - N
# print(" Iter {}: EFhalf = {:12.8f} dQhalf = {:12.4g}".format(i, EFhalf, dQhalf))
# EFの精度がepsより小さくなったら計算終了
if abs(EFmin - EFhalf) < eps and abs(EFmax - EFhalf) < eps:
# print(" Success: Convergence reached at EF = {}".format(EFhalf))
break
if dQmin * dQhalf < 0.0:
EFmax = EFhalf
dQmax = dQhalf
else:
EFmin = EFhalf
dQmin = dQhalf
else:
print(" Failed: Convergence did not reach")
exit()
return EFhalf
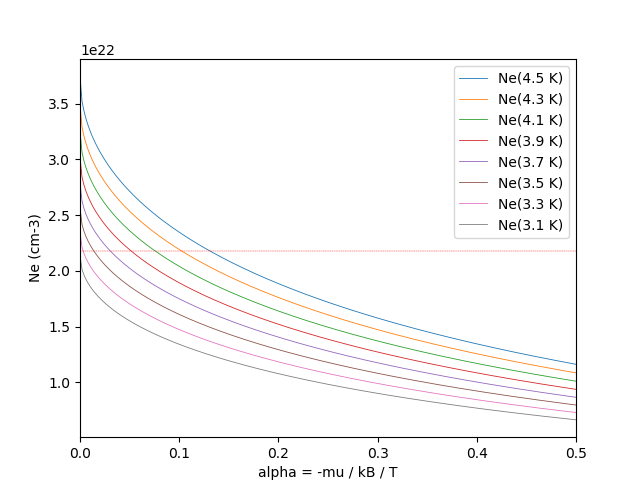
def ExecFs():
global m, zeta32
# グラフの準備
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_xlabel("alpha = -mu / kB / T")
ax1.set_ylabel("Ne (cm-3)")
for i in range(nT):
T = Tmax - i * Tstep
lambdaT = h / sqrt(2.0 * pi * m * kB * T)
Nmax = 1.0 / pow(lambdaT, 3.0) * zeta32 * 1.0e-6
print("T = %g K lamda_T = %g nm Nmax = %g cm-3" % (T, lambdaT * 1e9, Nmax))
print(" alpha\tmu(eV)\tFs\tNe(cm-3)")
xalpha = []
xEF = []
yFs = []
yNe = []
for ia in range(nalpha):
alpha = alphamin + ia * alphastep
EF = -alpha * kB * T / e
fs = Fsalpha(1.5, alpha)
ne = Ne(EF, T)
xEF.append(EF)
yFs.append(fs)
yNe.append(ne)
# print("%10.6f\t%10.6g\t%16.6g\t%16.6e" % (alpha, EF, fs, ne))
# 温度Tのグラフを追加
xalpha.append(alpha)
ax1.plot(xalpha, yNe, label = 'Ne(%g K)' % (T), linewidth = 0.6)
# Nの線を追加
ax1.plot([alphamin, alphamax], [N, N], color = 'red', linewidth = 0.3, linestyle = 'dashed')
ax1.set_xlim([alphamin, alphamax])
#=============================
# グラフの表示
#=============================
ax1.legend()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
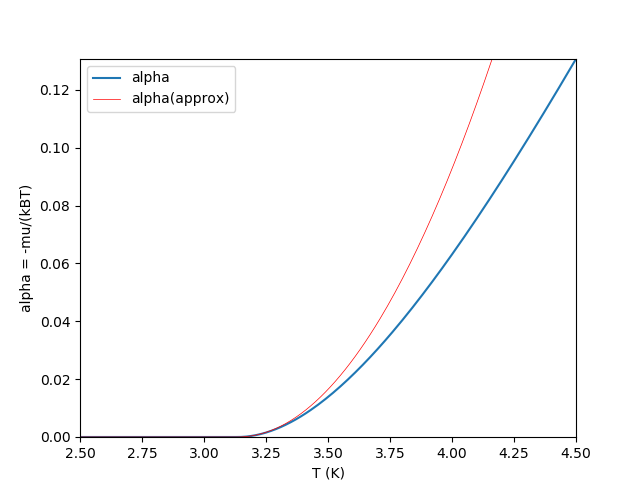
def ExecMu():
global m, zeta32
Tc = h * h / 2.0 / pi / m / kB * pow(N*1.0e6 / zeta32, 2.0/3.0)
xT = []
yEF = []
yEFapprox = []
print(" T(K) \tlambda_T(nm)\t EF(eV)\t Fapprox(eV)\t N'(cm-3)\t Nmax(cm-3)\t N0(cm-3)")
for i in range(nT):
T = Tmax - i * Tstep
lambdaT = h / sqrt(2.0 * pi * m * kB * T)
Nmax = 1.0 / pow(lambdaT, 3.0) * zeta32 * 1.0e-6
if T < Tc:
EF = 0.0
EFapprox = 0.0
# Ncal = Ne(EF, T, lambdaT)
# N0 = N - Ne(EF, T, lambdaT)
Ncal = N * pow(T / Tc, 1.5)
N0 = N - Ncal
print("%8.5f\t%8.4g\t%12.4g\t%12.4g\t%12.4e\t%12.4e\t%12.4e" % (T, lambdaT * 1.0e9, EF, EFapprox, Ncal, Nmax, N0))
else:
#初期範囲
EFmin = -2.0
EFmax = -1.0e-100
EF = CalEF(T, N, EFmin, EFmax)
t = (T - Tc) / Tc
Aapprox = 9.0 / 16.0 / pi * zeta32 * zeta32 * t * t
EFapprox = -Aapprox * kB * T / e
Ncal = Ne(EF, T)
print("%8.5f\t%8.4g\t%12.4g\t%12.4g\t%12.4e\t%12.4e" % (T, lambdaT * 1.0e9, EF, EFapprox, Ncal, Nmax))
xT.append(T)
yEF.append(-EF / (kB * T / e))
yEFapprox.append(-EFapprox / (kB * T / e))
#=============================
# グラフの表示
#=============================
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.plot(xT, yEF, label = 'alpha')
ax1.plot(xT, yEFapprox, label = 'alpha(approx)', linestyle = '-', linewidth = 0.5, color = 'red')
ax1.set_xlabel("T (K)")
ax1.set_ylabel("alpha = -mu/(kBT)")
ax1.set_xlim([Tmin, Tmax])
ax1.set_ylim([0.0, max(yEF)])
ax1.legend()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
def main():
global m, zeta32
zeta32 = Fsalpha(1.5, 0.0)
print("m = ", m, " kg")
print("N = ", N, " cm^-3")
print("")
print("G(1.5)=", Gamma(1.5))
print("F3/2(0)=", zeta32)
print("")
Tc = h * h / 2.0 / pi / m / kB * pow(N*1.0e6 / zeta32, 2.0/3.0)
print("Tc=", Tc, " K")
print("")
if mode == 'Fs':
ExecFs()
if mode == 'mu':
ExecMu()
if __name__ == '__main__':
main()