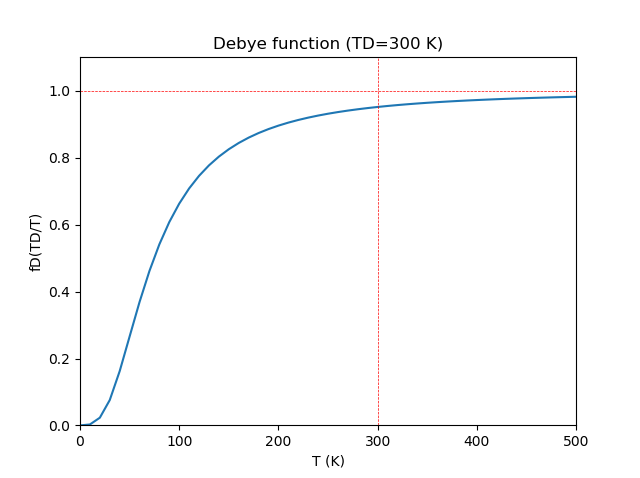
Calculate Debye function fD(y).
Mol const. V heat capacity: CV = 3R * fD(TD/T), where TD is the Debye temperature.
Download script from .\debye_function.py
import sys
import random
from math import exp
import numpy as np
from scipy import integrate # 数値積分関数 integrateを読み込む
from matplotlib import pyplot as plt
"""
Calculate Debye function fD(y).
Mol const. V heat capacity: CV = 3R * fD(TD/T), where TD is the Debye temperature.
"""
# Debye Temperature
TD = 300.0 # K
# Calculate T range
Tmin = 0.0
Tmax = 400.0
Tstep = 10.0
# Treat argments
argv = sys.argv
if len(argv) == 1:
print("Usage: python debye_function.py TD Tmin Tmax Tstep")
print(" e.g.: pythnon debye_function.py 300 0 500 10")
exit()
if len(argv) >= 2:
TD = float(argv[1])
if len(argv) >= 3:
Tmin = float(argv[2])
if len(argv) >= 4:
Tmax = float(argv[3])
if len(argv) >= 5:
Tstep = float(argv[4])
# 被積分関数を定義
def func(x):
expx = exp(x)
expx1 = expx - 1.0
return pow(x, 4) * expx / expx1 / expx1
def main():
T = []
fD = []
nT = int((Tmax - Tmin) / Tstep) + 1
print(" T(K) T/TD integ fD(T/TD)")
for i in range(nT):
Ti = Tmin + i * Tstep
T.append(Ti)
# 温度が 0 K のときは y=>∞ となって計算できないので、極限値 0 を与える
if Ti <= 0.0:
y = 0.0
fD.append(0.0)
integ = 0.0
else:
y = TD / Ti
ret = integrate.quad(func, 0.0, y)
integ = ret[0]
fD.append(3.0 / pow(y, 3) * integ)
print("%6.1f\t%6.4f\t%12.6g\t%8.4f" % (Ti, y, integ, fD[i]))
#=============================
# グラフの表示
#=============================
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.plot(T, fD)
ax1.plot([Tmin, Tmax], [1.0, 1.0], color = 'red', linestyle = 'dashed', linewidth = 0.5)
ax1.plot([TD, TD], [0.0, 1.1], color = 'red', linestyle = 'dashed', linewidth = 0.5)
ax1.set_title('Debye function (TD=%g K)' % (TD))
ax1.set_xlabel("T (K)")
ax1.set_ylabel("fD(TD/T)")
ax1.set_xlim([Tmin, Tmax])
ax1.set_ylim([0, 1.1])
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
if __name__ == '__main__':
main()