(i) download inside/MR-Hall/MR.py, inside/MR-Hall/MRxx.csv, and inside/MR-Hall/MRxy.csv
(ii) Run
     python MR.py
     and see Usage. 
  Usage: Variables in () are optional
    Units are in MKSA (e.g., nh0 and ne0 are in m^-3)
    [Bmin, Bmax] should be the same for xx and xy to keep consistency
  (i) python MR.py plot (model file_xx file_xy Bxxmin Bxxmin Bxxmin Bxxmin nh0 muh0 ne0 mue0)
    Plot the raw and the calculated data using the initial parameters
    mode: two, single
    ex: python MR.py plot two MRxx.csv MRxy.csv -20.0 20.0 -20.0 20.0 1.0e24 0.2 2.0e24 0.03
  (ii) python MR.py fit (model file_xx file_xy Bxxmin Bxxmin Bxxmin Bxxmin nh0 muh0 ne0 mue0 wxx wxy maxiter tol graphupdateinterval)
    Perform mode=fit, optimize the parameters, and plot the optimized data
    mode: two, single
    ex: python MR.py fit two MRxx.csv MRxy.csv -20.0 20.0 -20.0 20.0 1.0e24 0.2 2.0e24 0.03 1.0 1.0 1000 1.0e-4 10

(iii) E.g., run   
    python MR.py fit two MRxx.csv MRxy.csv -20.0 20.0 -20.0 20.0 1.0e24 0.2 2.0e24 0.03 1.0 1.0 1000 1.0e-4 10
   
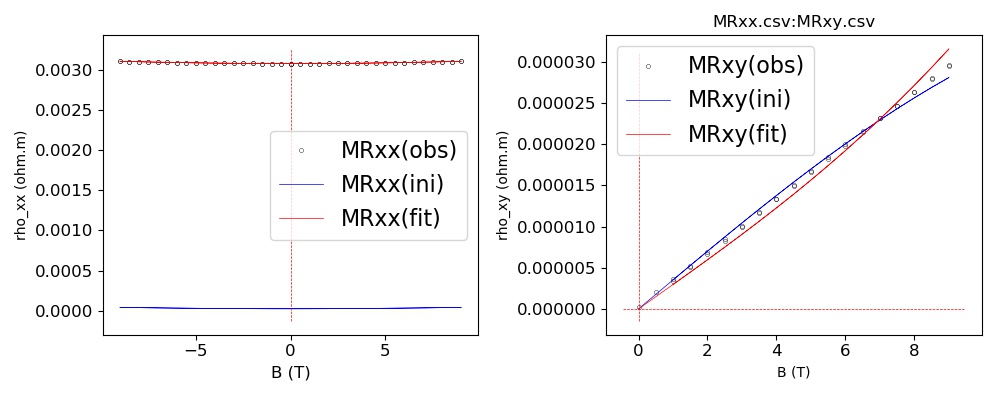
(iv) After press ENTER, you would see
  Next suggestion:
    python MR.py fit two MRxx.csv MRxy.csv -20.0 20.0 -20.0 20.0 3.025e+23 0.005649 1.325e+22 0.02411 1.0 1.0 1000 0.0001 10
(v) Run this line to continue the fitting using the previously-optimized parameters.
    python MR.py fit two MRxx.csv MRxy.csv -20.0 20.0 -20.0 20.0 3.025e+23 0.005649 1.325e+22 0.02411 1.0 1.0 1000 0.0001 10

  Optimized values 
    Failed: message from optimization: Maximum number of iterations has been exceeded.
       Hole : 2.52144e+23 m^-3 0.00641557 m^2/V/s
       Electron: 2.0103e+22 m^-3 0.0204162 m^2/V/s
       S2: 2.8200445268709547e-13

(vi) Check the lines below 'Optimized values'. The above example says 'Failed' as the required convergence criteria (tol) was not reached.
     This case, repeat (iv) - (v) until the convergence will be reached or the square sum of residual S2 will be small enough and unchange. 

import os
import sys
import csv
from math import exp, sqrt
import numpy as np
from numpy import arange
from scipy import integrate # 数値積分関数 integrateを読み込む
from scipy import optimize # newton関数はscipy.optimizeモジュールに入っている
from scipy.interpolate import interp1d
from scipy import optimize
from scipy.optimize import minimize
from matplotlib import pyplot as plt


"""
縦MR, 横MRから電子−正孔混合伝導のキャリア濃度、移動度をもとめる
最適化にはSIMPLEX法を使う

cf. Two carrier model for Hall resistance and magnetoresistance, APL 107, 182411 (2015)
"""


# constants
pi = 3.14159265358979323846
h = 6.6260755e-34 # Js";
hbar = 1.05459e-34 # "Js";
c = 2.99792458e8 # m/s";
e = 1.60218e-19 # C";
e0 = 8.854418782e-12; # C²N^-1m^-2";
kB = 1.380658e-23 # JK^-1";
me = 9.1093897e-31 # kg";


### Kamiya added
Debug = 0

# mode: 'plot', 'fit'
mode = 'plot'
# model: 'single', 'two', 'paraboric', 'same_mu'
model = 'two'

#Files
file_xx = 'MRxx.csv'
file_xy = 'MRxy.csv'

#フィッティング範囲
Bxxmin = -3.0
Bxxmax = 3.0
Bxymin = Bxxmin
Bxymax = Bxxmax
Bxx = []
MRxx = []
MRxxcal = []
Bxy = []
MRxy = []
MRxycal = []


#ρ(0)、正孔濃度、正孔移動度、電子濃度、電子移動度の初期値
nh0 = 3e23 # 2*1.35e24 # m^-3
muh0 = 0.006 # 2*0.200 # m^2/Vs
ne0 = 1.3e22 # 2*1.8e24 # m^-3
mue0 = 0.02 # 5*0.0300 # m^2/Vs

#ρxxとρxyの残差二乗和のweight。wxxは1.0に固定
wxx = 1.0
wxy = 100.0

#=============================================
# scipy.optimize.minimizeで使うアルゴリズム
#=============================================
#nelder-mead Downhill simplex
#powell Modified Powell
#cg conjugate gradient (Polak-Ribiere method)
#bfgs BFGS法
#newton-cg Newton-CG
#trust-ncg 信頼領域 Newton-CG 法
#dogleg 信頼領域 dog-leg 法
#L-BFGS-B’ (see here)
#TNC’ (see here)
#COBYLA’ (see here)
#SLSQP’ (see here)
#trust-constr’(see here)
#dogleg’ (see here)
#trust-exact’ (see here)
#trust-krylov’ (see here)
method = "nelder-mead"
#method = 'cg'
#method = 'powell'
#method = 'bfgs'

maxiter = 1000
tol = 1.0e-4
h_diff = 1.0e-3

#=============================
# Graph configuration
#=============================
fontsize = 12
legend_fontsize = 16
graphupdateinterval = 10

#=============================
# Treat argments
#=============================
def pfloat(str):
    try:
        return float(str)
    except:
        return None

def pint(str):
    try:
        return int(str)
    except:
        return None

def getarg(position, defval = None):
    try:
        return sys.argv[position]
    except:
        return defval

def getfloatarg(position, defval = None):
    return pfloat(getarg(position, defval))

def getintarg(position, defval = None):
    return pint(getarg(position, defval))

def usage():
    print("")
    print("Usage: Variables in () are optional")
    print(" Units are in MKSA (e.g., nh0 and ne0 are in m^-3)")
    print(" [Bmin, Bmax] should be the same for xx and xy to keep consistency")
    print(" (i) python {} plot (model file_xx file_xy Bxxmin Bxxmin Bxxmin Bxxmin nh0 muh0 ne0 mue0)"
                    .format(sys.argv[0]))
    print(" Plot the raw and the calculated data using the initial parameters")
    print(" mode: two, single")
    print(" ex: python {} plot two MRxx.csv MRxy.csv -20.0 20.0 -20.0 20.0 1.0e24 0.2 2.0e24 0.03"
                    .format(sys.argv[0]))
    print(" (ii) python {} fit (model file_xx file_xy Bxxmin Bxxmin Bxxmin Bxxmin nh0 muh0 ne0 mue0 wxx wxy maxiter tol graphupdateinterval)"
                    .format(sys.argv[0]))
    print(" Perform mode=fit, optimize the parameters, and plot the optimized data")
    print(" mode: two, single")
    print(" ex: python {} fit two MRxx.csv MRxy.csv -20.0 20.0 -20.0 20.0 1.0e24 0.2 2.0e24 0.03 1.0 1.0 1000 1.0e-4 10"
                    .format(sys.argv[0]))

def updatevars():
    global mode, model
    global file_xx, file_xy
    global Bxxmin, Bxxmax, Bxymin, Bxymax
    global nh0, muh0, ne0, mue0
    global wxx, wxy
    global maxiter, tol, graphupdateinterval

    argv = sys.argv
    if len(argv) == 1:
        usage()
        exit()

    mode = getarg( 1, mode)
    model = getarg( 2, model)
    file_xx = getarg( 3, file_xx)
    file_xy = getarg( 4, file_xy)
    Bxxmin = getfloatarg( 5, Bxxmin)
    Bxxmax = getfloatarg( 6, Bxxmax)
    Bxymin = getfloatarg( 7, Bxymin)
    Bxymax = getfloatarg( 8, Bxymax)
    nh0 = getfloatarg( 9, nh0)
    muh0 = getfloatarg(10, muh0)
    ne0 = getfloatarg(11, ne0)
    mue0 = getfloatarg(12, mue0)
    wxx = getfloatarg(13, wxx)
    wxy = getfloatarg(14, wxy)
    maxiter = getintarg (15, maxiter)
    tol = getfloatarg(16, tol)
    graphupdateinterval = getintarg(17, graphupdateinterval)


#=============================
# other functions
#=============================
def savecsv(outfile, header, datalist):
    try:
        print("Write to [{}]".format(outfile))
        f = open(outfile, 'w')
    except:
# except IOError:
        print("Error: Can not write to [{}]".format(outfile))
    else:
        fout = csv.writer(f, lineterminator='\n')
        fout.writerow(header)
# fout.writerows(data)
        for i in range(0, len(datalist[0])):
            a = []
            for j in range(len(datalist)):
                a.append(datalist[j][i])
            fout.writerow(a)
        f.close()

def read_csv(infile, xmin = None, xmax = None, delimiter = ','):
    print("xrange=", xmin, xmax)
    data = []
    try:
        infp = open(infile, "r")
        f = csv.reader(infp, delimiter = delimiter)
        header = next(f)
        print("header=", header)
        for j in range(len(header)):
            data.append([])

        for row in f:
            x = pfloat(row[0])
            if xmin is not None and xmin <= x <= xmax:
                y = pfloat(row[1])
                data[0].append(x)
                data[1].append(y)
    except:
        print("Error: Can not read [{}]".format(infile))
        exit()
    return header, data[0], data[1]


def MR_twocarrier(nh, muh, ne, mue, B):
    global e

    B2 = B * B
    muh2mue2 = muh * muh * mue * mue
    nhmuhnemue = nh * muh + ne * mue
    nhmuenemuh = nh * mue + ne * muh
    ndiff = nh - ne
    nmu2diff = nh * muh * muh - ne * mue * mue

    a1 = nhmuhnemue + nhmuenemuh * muh * mue * B2
    a2 = nhmuhnemue * nhmuhnemue + ndiff * ndiff * muh2mue2 * B2
    rhoxx = 1.0 / e * a1 / a2
    rhoxx0 = 1.0 / e / nhmuhnemue
    MRxx = rhoxx - rhoxx0

    a3a = nmu2diff # nh*muh*muh - ne*mue*mue
    a3b = ndiff * muh2mue2 * B2 # (nh - ne) * muh*muh*mue*mue * B2
    a4a = nhmuhnemue * nhmuhnemue # pow(nh*muh + ne*mue, 2)
    a4b = ndiff * ndiff * muh2mue2 * B2 #pow(nh - ne, 2) * muh*muh*mue*mue * B2
    a3 = a3a + a3b
    a4 = a4a + a4b
    MRxy = B / e * a3 / a4

    return rhoxx, rhoxx0, MRxx, MRxy

def MR_singlecarrier(n, mu, B):
    global e

    B2 = B * B
    sigmaxx0 = e * n * mu
# sigmaxx = sigmaxx0 * (1.0 + mu * mu * B2)
# rhoxx = 1.0 / sigmaxx
# rhoxx0 = 1.0 / sigmaxx0
    rhoxx0 = 1.0 / sigmaxx0
    rhoxx = rhoxx0 * (1.0 + mu * mu * B2)
    MRxx = rhoxx - rhoxx0

    MRxy = B / e / n

    return rhoxx, rhoxx0, MRxx, MRxy

def MR_samemu(nh, mu, ne, B):
    return MR_twocarrier(nh, mu, ne, mu, B)


def MR(model, nh, muh, ne, mue, B):
    if model == 'two':
        return MR_twocarrier(nh, muh, ne,mue, B)
    elif model == 'single':
        return MR_singlecarrier(nh, muh, B)
    elif model == 'same_mu':
        return MR_samemu(nh, muh, ne, B)

def calMRxxlist(model, B, nh, muh, ne, mue, IsPrint = 1):
    global MRxx

    if IsPrint:
        print("{}\t{}\t{}".format("B (T)", "MRxx (ohm.m)(obs)", "MRxx (ohm.m)(cal)"))
    MRxxcal = []
    for i in range(len(B)):
        rxx, rxx0, MR_xx, MR_xy = MR(model, nh, muh, ne, mue, B[i])
        MRxxcal.append(rxx)
# MRxxcal.append(MR_xx)
        if IsPrint:
            print("{}\t{}\t{}".format(B[i], MRxx[i], MRxxcal[i]))
    if IsPrint:
        print("")
    return MRxxcal

def calMRxylist(model, B, nh, muh, ne, mue, IsPrint = 1):
    global MRxy

    if IsPrint:
        print("{}\t{}\t{}".format("B (T)", "MRxy (ohm.m)(obs)", "MRxy (ohm.m)(cal)"))
    MRxycal = []
    for i in range(len(B)):
        rxx, rxx0, MR_x, MR_xy = MR(model, nh, muh, ne, mue, B[i])
        MRxycal.append(MR_xy)
        if IsPrint:
            print("{}\t{}\t{}".format(B[i], MRxy[i], MRxycal[i]))
    if IsPrint:
        print("")
    return MRxycal


def calS2(xk):
    global model
    global Bxx, MRxx, Bxy, MRxy

    if model == 'two':
        if xk[0] < 0.0 or xk[1] < 0.0 or xk[2] < 0.0 or xk[3] < 0.0:
            return 1.0e30

        nh = max([0.0, xk[0]])
        muh = max([0.0, xk[1]])
        ne = max([0.0, xk[2]])
        mue = max([0.0, xk[3]])
    elif model == 'single':
        if xk[1] < 0.0:
            return 1.0e30

        nh = xk[0]
        muh = max([0.0, xk[1]])
        ne, mue = 0.0, 0.0
    elif model == 'same_mu':
        if xk[0] < 0.0 or xk[1] < 0.0 or xk[2] < 0.0:
            return 1.0e30

        nh = max([0.0, xk[0]])
        muh = max([0.0, xk[1]])
        ne = max([0.0, xk[2]])
        mue = muh

    MRxxcal = calMRxxlist(model, Bxx, nh, muh, ne, mue, 0)
    MRxycal = calMRxylist(model, Bxy, nh, muh, ne, mue, 0)

    S2 = 0.0
    for i in range(len(Bxx)):
        S2 += wxx * pow(MRxxcal[i] - MRxx[i], 2)
    for i in range(len(Bxy)):
        S2 += wxy * pow(MRxycal[i] - MRxy[i], 2)
    return S2 / (wxx * len(Bxx) + wxy * len(Bxy))

# First derivatives to be used e.g. for cg method
# Approximate by forward difference method with the delta h = h_diff
def diff1(ai):
    n = len(ai)
    f0 = CalS2(ai)
    df = np.empty(n)
    for i in range(n):
        aii = ai
        aii[i] = ai[i] + h_diff
        df[i] = (CalS2(aii) - f0) / h_diff
    return df

# Update graph
def plot(fig, Bxx, MRxx, Bxy, MRxy, MRxxcal, MRxycal, MRxxfit = None, MRxyfit = None):
    global graphupdateinterval

    plt.clf()

    ax1 = fig.add_subplot(1, 2, 1)
    ax2 = fig.add_subplot(1, 2, 2)
    plt.title(file_xx + ':' + file_xy, fontsize = fontsize)

    ax1.plot(Bxx, MRxx, label = 'MRxx(obs)', linestyle = 'none', color = 'black',
                marker = 'o', markersize = 3.0, markerfacecolor = 'none', markeredgecolor = 'black', markeredgewidth = 0.3)
    ax1.plot(Bxx, MRxxcal, label = 'MRxx(ini)', linestyle = '-', color = 'blue', linewidth = 0.5)
    ax1.plot([0, 0], ax1.get_ylim(), color = 'red', linestyle = 'dashed', linewidth = 0.5)
# ax1.plot(ax1.get_xlim(), [0, 0], color = 'red', linestyle = 'dashed', linewidth = 0.5)

    ax2.plot(Bxy, MRxy, label = 'MRxy(obs)', linestyle = 'none', color = 'black',
                marker = 'o', markersize = 3.0, markerfacecolor = 'none', markeredgecolor = 'black', markeredgewidth = 0.3)
    ax2.plot(Bxy, MRxycal, label = 'MRxy(ini)', linestyle = '-', color = 'blue', linewidth = 0.5)
    ax2.plot([0, 0], ax2.get_ylim(), color = 'red', linestyle = 'dashed', linewidth = 0.5)
    ax2.plot(ax2.get_xlim(), [0, 0], color = 'red', linestyle = 'dashed', linewidth = 0.5)

    if MRxxfit is not None:
        ax1.plot(Bxx, MRxxfit, label = 'MRxx(fit)', linestyle = '-', color = 'red', linewidth = 0.5)
        ax2.plot(Bxy, MRxyfit, label = 'MRxy(fit)', linestyle = '-', color = 'red', linewidth = 0.5)

    ax1.set_xlabel("B (T)", fontsize = fontsize)
    ax1.set_ylabel("rho_xx (ohm.m)")
    ax2.set_xlabel("B (T)")
    ax2.set_ylabel("rho_xy (ohm.m)")
    ax1.legend(fontsize = legend_fontsize)
    ax2.legend(fontsize = legend_fontsize)
    ax1.tick_params(labelsize = fontsize)
    ax2.tick_params(labelsize = fontsize)
    plt.tight_layout()
    plt.pause(0.001)

# Callback function for scipy.optimize.minimize()
# Print variables every iteration, and update graph for every graphupdateinterval iterationsおｔ
iter = 0
def callback(fig, xk):
    global model
    global iter
    global Bxx, Bxy
    global MRxxcal, MRxycal

    S2 = calS2(xk)
    if model == 'two':
        nh, muh, ne, mue = xk
    elif model == 'single':
        nh, muh = xk
        ne, mue = 0.0, 0.0
    elif model == 'same_mu':
        nh, muh, ne = xk
        mue = muh

# パラメータと残差二乗和を表示
    print("callback {}: nh={:14.4g} muh={:10.4g} ne={:14.4g} mue={:10.4g} S2={:12.6g}"
            .format(iter, nh, muh, ne, mue, S2))
    iter += 1

# Update graphs
    if iter % graphupdateinterval == 0:
        MRxxfit = calMRxxlist(model, Bxx, nh, muh, ne, mue, 0)
        MRxyfit = calMRxylist(model, Bxy, nh, muh, ne, mue, 0)
        plot(fig, Bxx, MRxx, Bxy, MRxy, MRxxcal, MRxycal, MRxxfit, MRxyfit)


def main():
    global mode, model
    global nh0, muh0, ne0, mue0
    global Bxx, MRxx, Bxy, MRxy, MRxxcal, MRxycal
    global wxx, wxy

    updatevars()

    print("")
    print("mode : ", mode)
    print("model: ", model)
    print("MR_xx file : ", file_xx)
    print("MR_xy file : ", file_xy)
    print(" Read [{}]".format(file_xx))
    headerxx, Bxx, MRxx = read_csv(file_xx, Bxxmin, Bxxmax)
    print(" Bxx range: {} - {}".format(Bxxmin, Bxxmax))
    print(" Bxy range: {} - {}".format(Bxymin, Bxymax))
    print(" Read [{}]".format(file_xy))
    headerxy, Bxy, MRxy = read_csv(file_xy, Bxymin, Bxymax)
    print("Initial values")
    print(" Hole : {:12.6g} m^-3 {:12.6g} m^2/V/s".format(nh0, muh0))
    print(" Electron: {:12.6g} m^-3 {:12.6g} m^2/V/s".format(ne0, mue0))
    print("")
    print("Optimization configuration")
    print(" weight for rho_xx (wxx): ", wxx)
    print(" weight for rho_xy (wxy): ", wxy)
    print(" method: ", method)
    print(" maxiter: ", maxiter)
    print(" tol : ", tol)
    print("")
    print("Graph configuration")
    print(" Update every {} iterations".format(graphupdateinterval))

#変数のリスト
    if model == 'two':
        ai0 = [nh0, muh0, ne0, mue0]
    elif model == 'single':
        ai0 = [nh0, muh0]
        ne0 = 0.0
        mue0 = 0.0
    elif model == 'same_mu':
        ai0 = [nh0, muh0, ne0]
        mue0 = muh0
    else:
        print("")
        print("*** ERROR: Invalid model [{}]".format(model))
        print("")
        usage()
        exit()

    print("")
    print("Calculated from the initial parameters")
    S2 = calS2([nh0, muh0, ne0, mue0])
    print(" S2=", S2)
    MRxxcal = calMRxxlist(model, Bxx, nh0, muh0, ne0, mue0, 1)
    MRxycal = calMRxylist(model, Bxy, nh0, muh0, ne0, mue0, 1)

# Plot graphs
    fig = plt.figure(figsize = (10, 4))
    plot(fig, Bxx, MRxx, Bxy, MRxy, MRxxcal, MRxycal)

    if mode == 'plot':
        print("Press ENTER to exit>>", end = '')
        input()
        exit()

#=============================
# Optimization
#=============================
    print("")
    print("Optimization by ", method)
    print(" tol=", tol)

    ret = minimize(calS2, ai0, method = method, jac = diff1, tol = tol, callback = lambda xk: callback(fig, xk),
                options = {'maxiter':maxiter, "disp":True})
    print("ret=", ret)

    if method == 'nelder-mead':
        simplex = ret['final_simplex']
        ai = simplex[0][0]
        fmin = ret['fun']
    elif method == 'cg':
        ai = ret['x']
        fmin = ret['fun']
    elif method == 'powell':
        ai = ret['x']
        fmin = ret['fun']
    elif method == 'bfgs':
        ai = ret['x']
        fmin = CalS2(ai)

    if model == 'two':
        nh, muh, ne, mue = ai
    elif model == 'single':
        nh, muh = ai
        ne, mue = 0.0, 0.0
    elif model == 'same_mu':
        nh, muh, ne = ai
        mue = muh

    print("")
    print("Calculated from the optimized parameters")
    MRxxfit = calMRxxlist(model, Bxx, nh, muh, ne, mue, 1)
    MRxyfit = calMRxylist(model, Bxy, nh, muh, ne, mue, 1)

    print("")
    print("Optimized values")
    if ret['success'] == False:
        print(" Failed: message from optimization: ", ret['message'])
    else:
        print(" Succeeded: message from optimization: ", ret['message'])
    print(" Hole : {:12.6g} m^-3 {:12.6g} m^2/V/s".format(nh, muh))
    print(" Electron: {:12.6g} m^-3 {:12.6g} m^2/V/s".format(ne, mue))
    print(" S2: ", fmin)
    print("")

# Plot final graphs
    plot(fig, Bxx, MRxx, Bxy, MRxy, MRxxcal, MRxycal, MRxxfit, MRxyfit)

    if mode == 'fit':
        print("Press ENTER to exit>>", end = '')
        input()

    print("")
    usage()

    if mode == 'fit':
        print("")
        print("Next suggestion:")
        print(" python {} {} {} {} {} {} {} {} {} {:10.4g} {:10.4g} {:10.4g} {:10.4g} {} {} {} {} {}"
                    .format(sys.argv[0], mode, model, file_xx, file_xy, Bxxmin, Bxxmax, Bxymin, Bxymax,
                            nh, muh, ne, mue, wxx, wxy, maxiter, tol, graphupdateinterval))
        print("")

    exit()


if __name__ == '__main__':
    main()