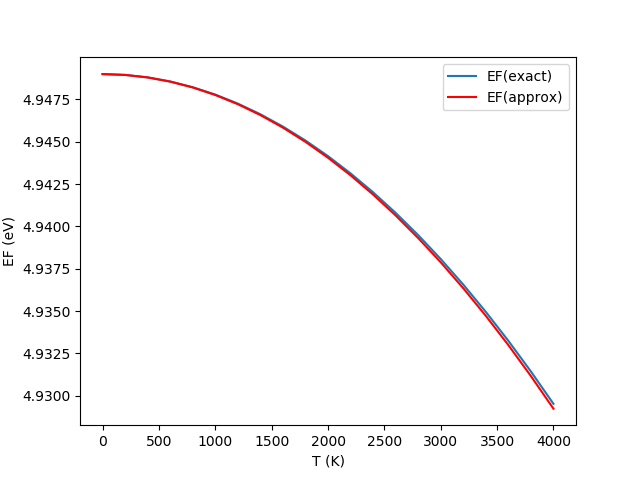
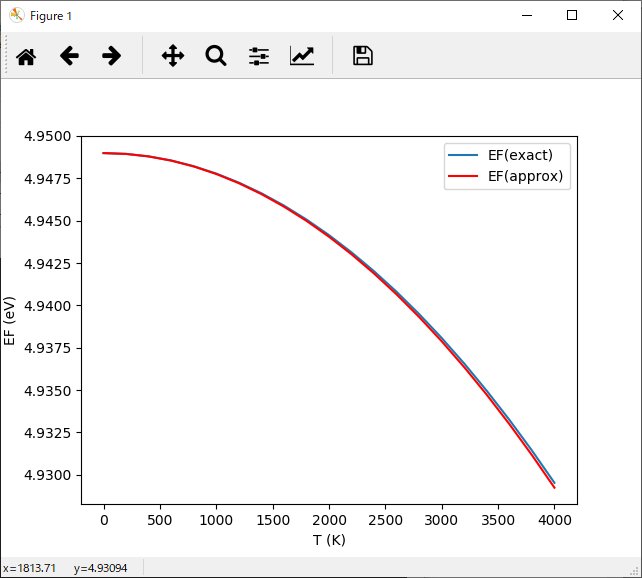
金属のEFの温度依存性を数値積分とNewton法で計算。
近似式と比較。
Calculate EF(T) for metal using numerical integration and the Newton method,
and compare with the approximation formula
Download script from .\EF-T-metal.py
import sys
import time
from math import exp, sqrt
import numpy as np
from scipy import integrate # 数値積分関数 integrateを読み込む
from scipy import optimize # newton関数はscipy.optimizeモジュールに入っている
from matplotlib import pyplot as plt
"""
金属のEFの温度依存性を数値積分とNewton法で計算。
近似式と比較。
Calculate EF(T) for metal using numerical integration and the Newton method,
and compare with the approximation formula
"""
# constants
pi = 3.14159265358979323846
h = 6.6260755e-34 # Js";
hbar = 1.05459e-34 # "Js";
c = 2.99792458e8 # m/s";
e = 1.60218e-19 # C";
kB = 1.380658e-23 # JK-1";
me = 9.1093897e-31 # kg";
# spin, effective mass, electron density
S = 1.0 / 2.0
m = 1.0
N = 5.0e22 # cm^-3
# Temperature range
Tmin = 0 # K
Tmax = 4000
Tstep = 200
nT = int((Tmax - Tmin) / Tstep + 1)
# integration will be performed in the range
# from EF - nrange * kBT to EF + nrange * kBT
nrange = 6.0
# Relative accuracy of the quad functin
eps = 1.0e-8
# Treat argments
argv = sys.argv
if len(argv) >= 2:
N = float(argv[1])
if len(argv) >= 3:
m = float(argv[2])
D0 = (2.0 * S + 1.0) * 2.0 * pi * pow(2.0*m, 1.5) / h / h / h # m^-3J^-1.5
D0 *= 1.0e-6 * pow(e, 1.5) # m^-3J^-1.5 => cm-3eV^-1.5
# Density-Of-States function
def De(E):
global D0
if E < 0.0:
return 0.0
return D0 * sqrt(E)
# Fermi-Dirac distribution function
def fe(E, T, EF):
global e, kB
if T == 0.0:
if E < EF:
return 1.0
else:
return 0.0
return 1.0 / (exp((E - EF) * e / kB / T) + 1.0)
# Define the function to be integrated
def Defe(E, T, EF):
return De(E) * fe(E, T, EF)
# Calculate electron density with a given EF
# For E < EF - dE, use the analytical integration
# For E > EF - dE, use the numerical integration with quad
# The upper limit of integration is determined as EF + dE
def Ne(T, EF, dE):
global D0, eps
(Emin, Emax) = (0.0, EF - dE)
Ne1 = 2.0 / 3.0 * D0 * (pow(Emax, 1.5) - pow(Emin, 1.5))
(Emin, Emax) = (EF - dE, EF + dE)
if Emin < 0.0:
Emin = 0.0
ret = integrate.quad(lambda E: Defe(E, T, EF), Emin, Emax, epsrel = eps)
return Ne1 + ret[0]
# Calculate EF base on
# the charge neutrality (electron number) condition, Ne(T, EF, dE) - N = 0,
# using the Newton method with the initial value EF0
def CalEF(N, T, EF0, dE):
global D0
if T == 0.0:
return pow(1.5 / D0 * N, 2.0 / 3.0) # eV
EF = optimize.newton(lambda EF: Ne(T, EF, dE) - N, EF0)
return EF
def main():
global m, D0
print("m = %g me" % (m))
m *= me
# Calculate the prefactor of De(E)
D0 = (2.0 * S + 1.0) * 2.0 * pi * pow(2.0*m, 1.5) / h / h / h # m^-3J^-1.5
D0 *= 1.0e-6 * pow(e, 1.5) # m^-3J^-1.5 => cm-3eV^-1.5
print("")
# EF at 0 K, to be used for the initial value of the Newton method
EF0 = pow(1.5 / D0 * N, 2.0 / 3.0) # eV
N0 = Ne(0.0, EF0, 0.0)
print("EF at 0K = ", EF0, " eV")
print("Ne at 0K = ", N0, " cm-3")
print("")
xT = []
yEF = []
yEFa = []
EFprev = EF0
print(" T(K) \t EF(eV) \tEFapprox(eV)\tNcheck(cm-3)")
for i in range(nT):
T = Tmin + i * Tstep
kBTe = kB * T / e
# Calculate the range of numerical integration
dE = nrange * kBTe
EF = CalEF(N, T, EFprev, dE)
Ncheck = Ne(T, EF, dE)
Ndiff = 1.0 / 2.0 * D0 * pow(EF0, -1.0 / 2.0)
EFapprox = EF0 - pi * pi / 6.0 * pow(kBTe, 2.0) * Ndiff / De(EF0)
xT.append(T)
yEF.append(EF)
yEFa.append(EFapprox)
print("%8.4f\t%10.6f\t%10.6f\t%16.6g" % (T, EF, EFapprox, Ncheck))
EFprev = EF
#=============================
# Plot graphs
#=============================
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.plot(xT, yEF, label = 'EF(exact)')
ax1.plot(xT, yEFa, label = 'EF(approx)', color = 'red')
ax1.set_xlabel("T (K)")
ax1.set_ylabel("EF (eV)")
ax1.legend()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
if __name__ == '__main__':
main()