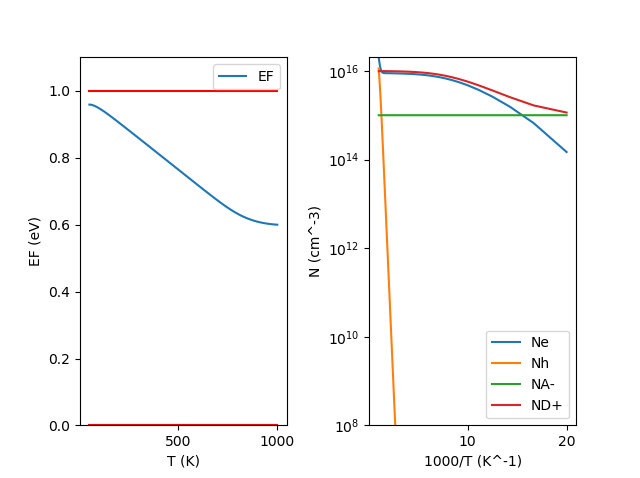
非縮退半導体のEFの温度依存性を二分法で計算。
Download script from .\EF-T-semiconductor.py
import sys
import numpy as np
from numpy import sin, cos, tan, pi, exp
from matplotlib import pyplot as plt
"""
非縮退半導体のEFの温度依存性を二分法で計算。
"""
#定数
e = 1.60218e-19 # C";
kB = 1.380658e-23 # JK-1";
# semiconductor parameters
#価電子帯上端エネルギー eV
Ev = 0.0
#伝導帯下端エネルギー
Ec = 1.0
#価電子帯有効状態密度
Nv = 1.2e19
#伝導帯有効状態密度
Nc = 2.1e18
#アクセプター準位
EA = 0.05
#アクセプター密度 cm-3
NA = 1.0e15
#ドナー準位
ED = Ec - 0.05
#ドナー密度
ND = 1.0e16
# Temperature range
Tmin = 50 # K
Tmax = 1000
Tstep = 10
nT = int((Tmax - Tmin) / Tstep + 1)
# Treat argments
argv = sys.argv
if len(argv) <= 1:
print("usage: python EF-T-semiconductor.py EA NA ED ND Ec Nv Nc")
print(" ex: python EF-T-semiconductor.py 0.05 1.0e15 0.95 1.0e16 1.0 1.2e19 2.1e18")
exit()
if len(argv) >= 2:
EA = float(argv[1])
if len(argv) >= 3:
NA = float(argv[2])
if len(argv) >= 4:
ED = float(argv[3])
if len(argv) >= 5:
ND = float(argv[4])
if len(argv) >= 6:
Ec = float(argv[5])
if len(argv) >= 7:
Nv = float(argv[6])
if len(argv) >= 8:
Nc = float(argv[7])
#EFの誤差がepsより小さくなったら計算終了
eps = 1.0e-5
#二分法の最大繰り返し数
nmaxiter = 200
#繰り返し中に途中経過を出力するサイクル数
iprintiterval = 1
# Fermi-Dirac function
def fe(E, EF, T):
global e, kB
if T == 0.0:
if E < EF:
return 1.0
else:
return 0.0
return 1.0 / (exp((E - EF) * e / kB / T) + 1.0)
# electron density
def Ne(EF, T):
global Nc, Ec, e, kB
if T == 0.0:
return 0.0
return Nc * exp(-(Ec - EF) * e / kB / T)
# hole density
def Nh(EF, T):
global Nv, Ev, e, kB
if T == 0.0:
return 0.0
return Nv * exp(-(EF - Ev) * e / kB / T)
# ionized donor density
def NDp(EF, T):
global ND, ED, kB
return ND * (1.0 - fe(ED, EF, T))
# ionized acceptor density
def NAm(EF, T):
global NA, EA, kB
return NA * fe(EA, EF, T)
def main():
global EFmin, EFmax, eps, nmaxiter, iprintinterval
print("Solution of EF by bisection method")
print("Ev=%f Ec=%f eV" % (Ev, Ec))
print("Nv=%e Nc=%e cm-3" % (Nv, Nc))
print("NA=%f cm-3 EA=%f eV" % (NA, EA))
print("ND=%f cm-3 ED=%f eV" % (ND, ED))
print("")
xT = []
xInvT = []
yEF = []
yNe = []
yNh = []
yNAm = []
yNDp = []
print(" T(K) \t EF(eV)\tNe(cm-3)\tNh(cm-3)\tNA+(cm-3)\tND-(cm-3)")
for iT in range(nT):
T = Tmin + iT * Tstep
#初期範囲として、価電子帯上端と伝導帯下端エネルギーを設定する
EFmin = Ev - 1.0
EFmax = Ec + 1.0
# まず、EFmin,EFmaxにおけるΔQを計算し、それぞれが正・負あるいは負・生となっていることを確認する
dQmin = Ne(EFmin, T) + NAm(EFmin, T) - Nh(EFmin, T) - NDp(EFmin, T)
dQmax = Ne(EFmax, T) + NAm(EFmax, T) - Nh(EFmax, T) - NDp(EFmax, T)
# print(" EFmin = {:12.8f} dQmin = {:12.4g}".format(EFmin, dQmin))
# print(" EFmax = {:12.8f} dQmax = {:12.4g}".format(EFmax, dQmax))
if dQmin * dQmax > 0.0:
print("Error: Initial Emin and Emax should be chosen as dQmin * dQmax < 0")
return 0
# 2分法開始
for i in range(nmaxiter):
EFhalf = (EFmin + EFmax) / 2.0
Neh = Ne(EFhalf, T)
NAmh = NAm(EFhalf, T)
Nhh = Nh(EFhalf, T)
NDph = NDp(EFhalf, T)
dQhalf = Neh + NAmh - Nhh - NDph
# print(" Iter {}: EFhalf = {:12.8f} dQhalf = {:12.4g}".format(i, EFhalf, dQhalf))
# print(" Ne={:10.4e} Nh={:10.4e} NA-={:10.4e} ND+={:10.4e} dQ={:10.4e}".format(Neh, Nhh, NAmh, NDph, dQhalf))
# EFの精度がepsより小さくなったら敬さん終了
if abs(EFmin - EFhalf) < eps and abs(EFmax - EFhalf) < eps:
# print(" Success: Convergence reached at EF = {}".format(EFhalf))
break
if dQmin * dQhalf < 0.0:
EFmax = EFhalf
dQmax = dQhalf
else:
EFmin = EFhalf
dQmin = dQhalf
else:
print(" Failed: Convergence did not reach")
return 0
xT.append(T)
xInvT.append(1000.0 / T)
yEF.append(EFhalf)
yNe.append(Neh)
yNh.append(Nhh)
yNAm.append(NAmh)
yNDp.append(NDph)
print("%8.4f\t%10.6f\t%12.4g\t%12.4g\t%12.4g\t%12.4g" % (T, EFhalf, Neh, Nhh, NAmh, NDph))
#=============================
# グラフの表示
#=============================
fig = plt.figure()
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
ax1.plot(xT, yEF, label = 'EF')
ax1.plot([Tmin, Tmax], [Ev, Ev], color = 'red')
ax1.plot([Tmin, Tmax], [Ec, Ec], color = 'red')
ax1.set_xlabel("T (K)")
ax1.set_ylabel("EF (eV)")
ax1.set_ylim([Ev, Ec * 1.1])
ax1.legend()
ax2.plot(xInvT, yNe, label = 'Ne')
ax2.plot(xInvT, yNh, label = 'Nh')
ax2.plot(xInvT, yNAm, label = 'NA-')
ax2.plot(xInvT, yNDp, label = 'ND+')
ax2.set_yscale("log")
ax2.set_xlabel("1000/T (K^-1)")
ax2.set_ylabel("N (cm^-3)")
maxy = max([max(yNe), max(yNh), max(yNAm), max(yNDp)])
ax2.set_ylim([1.0e8, maxy])
ax2.legend()
plt.subplots_adjust(wspace=0.4, hspace=0.6)
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
if __name__ == "__main__":
main()