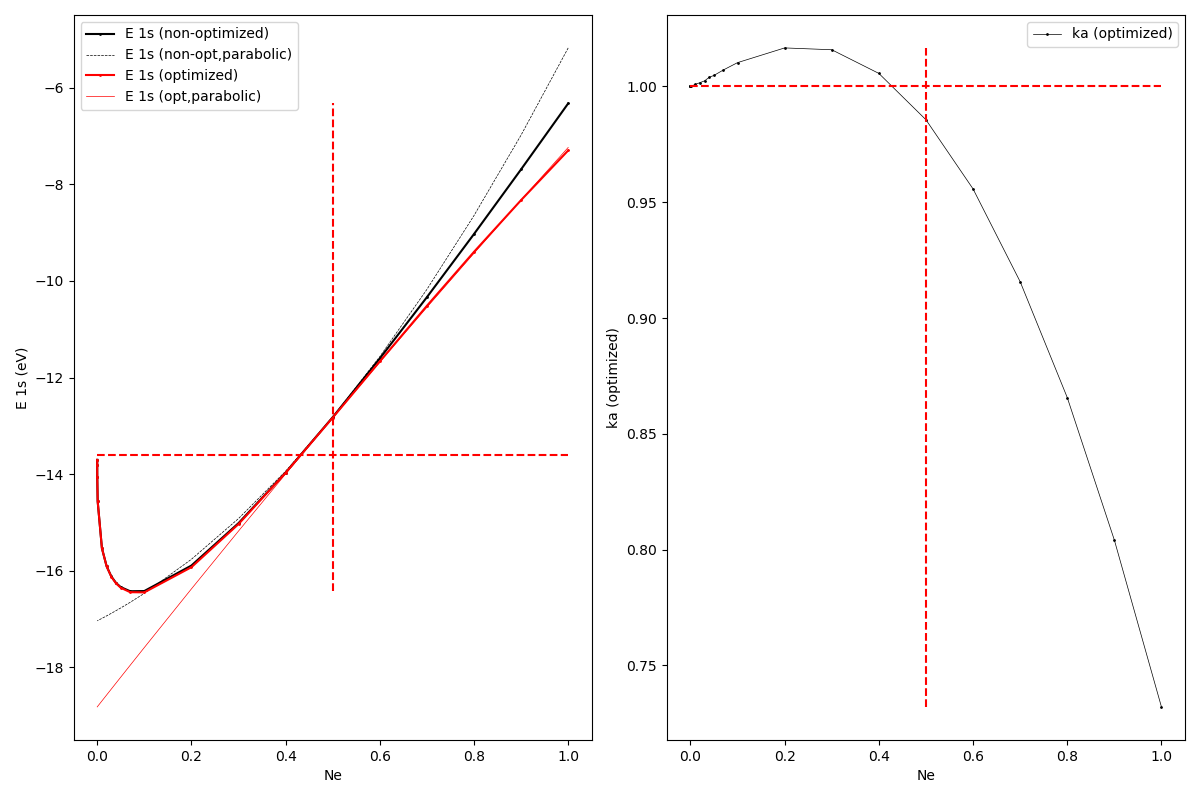
Calculate energy level of H-like 1s orbital
using 1s radial function and Slator's X-alpha potential
Download script from H1s-HF-LDA.py
import os
import sys
from math import exp, sqrt
import numpy as np
from math import log, exp
from numpy import arange
from scipy import integrate # 数値積分関数 integrateを読み込む
from scipy.interpolate import interp1d
from scipy import optimize
from scipy.optimize import minimize
from matplotlib import pyplot as plt
"""
Calculate energy level of H-like 1s orbital
using 1s radial function and Slator's X-alpha potential
"""
# constants
pi = 3.14159265358979323846
h = 6.6260755e-34 # Js";
hbar = 1.05459e-34 # "Js";
c = 2.99792458e8 # m/s";
e = 1.60218e-19 # C";
kB = 1.380658e-23 # JK-1";
me = 9.1093897e-31 # kg";
e0 = 8.854418782e-12; # C2N-1m-2";
e2_4pie0 = 2.30711e-28 # Nm2";
a0 = 5.29177e-11 * 1.0e10 # A
HartreeToeV = 27.2116 # eV";
RyToeV = HartreeToeV / 2.0
pi2 = pi + pi
pi4 = pi2 + pi2
# mode: 'd': debug mode, plot fundamental graphs
# 'g': plot graph
# 'k': sweep ka, 'n': sweep Ne
# 'v': add variational calculation, 'e': energy-based output
mode = 'k'
ELabel = 'E 1s'
# Nuclear and orbital parameters
Z = 1.0
n = 1
l = 0
m = 0
ka = 1.0 # coefficient of the exponent in R1s
Ne = 1.0
# Number of electrons, Slater's alpha
alpha = 2.0 / 3.0
# Radius range and integration (quad()) parameters
Rmin = 0.0
Rmax = 20.0
nR = 2001
Rstep = None
Rmaxdata = None
nmaxdiv = 40
epsR = 1.0e-4
eps = 1.0e-8
# Ne mesh to calculate 1st and 2nd derivative of Etot
hparab = 0.01
# iteration parameters
#Nearray = [1.0, 0.8, 0.6]
#Nearray = [1.0, 0.8, 0.6, 0.5, 0.4, 0.3, 0.1, 0.01, 0.001]
Nearray = [1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.07, 0.05, 0.04, 0.03, 0.02, 0.01, 1.0e-3, 1.0e-4, 1.0e-5, 1.0e-6]
kaarray = [0.5, 0.6, 0.65, 0.7, 0.8, 0.9, 0.95, 1.0, 1.05, 1.1, 1.2, 1.4]
#=============================================
# scipy.optimize.minimizeで使うアルゴリズム
#=============================================
#nelder-mead Downhill simplex
#powell Modified Powell
#cg conjugate gradient (Polak-Ribiere method)
#bfgs BFGS法
#newton-cg Newton-CG
#trust-ncg 信頼領域 Newton-CG 法
#dogleg 信頼領域 dog-leg 法
#L-BFGS-B’ (see here)
#TNC’ (see here)
#COBYLA’ (see here)
#SLSQP’ (see here)
#trust-constr’(see here)
#dogleg’ (see here)
#trust-exact’ (see here)
#trust-krylov’ (see here)
method = "nelder-mead"
#method = 'cg'
#method = 'powell'
#method = 'bfgs'
maxiter = 1000
tol = 1.0e-3
h_diff = 1.0e-3
# 実数値に変換できない文字列をfloat()で変換するとエラーになってプログラムが終了する
# この関数は、変換できなかったらNoneを返すが、プログラムは終了させない
def pfloat(str):
try:
return float(str)
except:
return None
# pfloat()のint版
def pint(str):
try:
return int(str)
except:
return None
# 起動時引数を取得するsys.argリスト変数は、範囲外のindexを渡すとエラーになってプログラムが終了する
# getarg()では、範囲外のindexを渡したときは、defvalを返す
def getarg(position, defval = None):
try:
return sys.argv[position]
except:
return defval
# 起動時引数を実数に変換して返す
def getfloatarg(position, defval = None):
return pfloat(getarg(position, defval))
# 起動時引数を整数値に変換して返す
def getintarg(position, defval = None):
return pint(getarg(position, defval))
def usage(ka = ka, Z = Z, n = n, l = l, m = m):
print("")
print("Usage: Variables in () are optional")
print(" (i) python {} mode Z ka Ne".format(sys.argv[0]))
print(" mode: combination of the following key characters")
print(" d: debug mode, plot fundamental graphs")
print(" v: add variational calculations")
print(" e: output based on energy (default: based on E 1s eigen value)")
print(" k: sweep ka")
print(" n: sweep Ne")
print(" g : plot graph")
print(" ex: python {} nvg {} {} {}".format(sys.argv[0], Z, ka, Ne))
print(" ex: python {} k {} {} {}".format(sys.argv[0], Z, ka, Ne))
def terminate(message = None):
if message is not None:
print("")
print(message)
usage()
print("")
exit()
# 起動時引数を使ってglobal変数を更新する
def updatevars():
global mode, ELabel
global ka, Z, Ne, n, l, m, Ne, Rmax, Rstep
argv = sys.argv
if len(argv) == 1:
terminate()
mode = getarg( 1, mode)
Z = getfloatarg( 2, Z)
ka = getfloatarg( 3, ka)
Ne = getfloatarg( 4, Ne)
if 'e' in mode:
ELabel = 'Etot'
else:
ELabel = 'E 1s'
# Total charge inside r
yRr = [] # Raidal distributuion function
yQr = [] # Integrated charge inside r: integ_rm(4pi * rm * rm * rho(rm))_[rm = 0, r]
# Radial distribution function of H-like 1s orbital
# Normalized by integ(4pi*r*r*Rr(r)*Rr(r))[r=0, inf] = 1
R1s0 = 2.0 / sqrt(4.0 * pi)
def Rr(ka, Z, n, l, m, r):
global R1s0
return R1s0 * pow(ka * Z, 1.5) * exp(-ka * Z * r)
def rho(ka, Z, n, l, m, r):
psi = Rr(ka, Z, n, l, m, r)
return psi * psi
# Integrated charge inside r: integ_rm(4pi * rm * rm * rho(rm))_[rm = 0, r]
qfunc = None
def calQ(R):
global Rmin, Rmaxdata, r, Qr
if R < Rmin:
print("Error in Q(r): Given r={} exceeds the R range [{}, {}]".format(R, Rmin, Rmax))
exit()
if R > Rmaxdata:
return 0.0
return qfunc(R)
def build_Qr(ka, Z, n, l, m):
global yRr, yQr, qfunc
yRr = []
yQr = []
for i in range(len(r)):
yRr.append(Rr(ka, Z, n, l, m, r[i]))
if r[i] == 0.0:
Q = 0.0
else:
Q, errQ = integrate.quad(lambda r: pi4 * r * r * rho(ka, Z, n, l, m, r), 0, r[i], limit = nmaxdiv, epsrel = eps)
yQr.append(Ne * Q)
qfunc = interp1d(r, yQr, kind = 'cubic')
def calTanal(Z = 1.0, ka = 1.0):
# T = e^2 / 8pi / e0 / a0
Tanal = Z * Z * ka * ka * e / 8.0 / pi / e0 / (a0*1.0e-10)
return Tanal
def calUanal(Z = 1.0, ka = 1.0):
# U = -e^2 / 4pi / e0 / a0
Uanal = -Z * Z * ka * ka * e / 4.0 / pi / e0 / (a0*1.0e-10)
return Uanal
# not used. for faster integration in future
def integrate_trapezoidal(func, E0, E1, h):
n = int((E1 - E0) / h + 1.000001)
h = (E1 - E0) / n
y = [func(E0 + i * h) for i in range(n)]
S = 0.5 * (y[0] + y[n-1]) + sum(y[1:n-1])
return [h * S, -1.0]
def integrate3DR(func, rmin, rmax, limit = 15, epsrel = 1.0e-8):
I, err = integrate.quad(lambda r: pi4 * r * r * func(r), rmin, rmax, limit, epsrel)
return I, err
# Electrostatic potential from nuclear
def calUZ(r, Z):
if r < 1.0e-3:
return -Z / 1.0e-3
else:
return -Z / r
# Electrostatic potential formed at r by distributed charge density rho(r)
def calUrho(r, ka, Z, n, l, m):
# Uerho(r) = integ(rho(m) / |r-rm|)_[rm=0, inf] [r, rm are vectors]
# = Q(r) / r + integ[4pi * rm * rm * rho(rm) / rm]_[rm = r, inf]) [r is vector]
if r == 0.0:
Uee1 = 0.0
else:
Uee1 = calQ(r) / r
Rmaxint = Rmax
# Rmaxint = min(-log(eps) / Z / ka, Rmax)
Uee2, errUee2 = integrate.quad(lambda rm: pi4 * rm * rho(ka, Z, n, l, m, rm), r, Rmaxint, limit = nmaxdiv, epsrel = eps)
return Uee1 + Uee2
# return Uee1 + Ne * Uee2
# Kinetic energy
# -1 / 2 * integ(4pi*r*r*R(r) * laplasian(R(r)))
# laplasian(Rr(r)) / R1s0 = 1/r^2 * d/dr[r^2dRr/dr] = 1/r^2 *d/dr[-Z * r^2*exp(-Zr)]
# = -Z / r^2 * [2r - Z * r*r]*exp(-Zr)
# r*r*R(r) * laplasian(R(r)) = -R1s0 * R1s0 * Z * r * [2 - Z * r] * exp(-2Zr)
def calT(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps):
Rmaxint = min(-log(eps) / Z / ka, Rmax)
T, errT = integrate.quad(lambda r: r * (2.0 - Z * ka * r) * exp(-2.0 * Z * ka * r),
Rmin, Rmaxint, limit = nmaxdiv, epsrel = eps)
T *= 1.0 / 2.0 * pi4 * Z * ka * R1s0 * R1s0 * pow(ka * Z, 3.0)
return T, errT
# UeZ = integ(4pi * r*r * (-(Z / r) * rho(r))
# = -Z * 4pi * integ(r * rho(r))
def calUeZ(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps):
Rmaxint = min(-log(eps) / Z / ka, Rmax)
UeZ, errUeZ = integrate.quad(lambda r: pi4 * r * rho(ka, Z, n, l, m, r),
Rmin, Rmaxint, limit = nmaxdiv, epsrel = eps)
UeZ *= -Z
return UeZ, errUeZ
# Uee = integ_r( integ_rm(rho(rm)/|rm-r|) * rho(r) ) [r and rm are vectors]
# = integ_r(4pi * r * r * Urho(r) * rho(r))_[r=0, inf] [r is scalar]
# Urho(r) = Q(r) / r + integ[4pi * rm * rm * rho(rm) / rm]_[rm = r, inf])
def calUee(mode, ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps):
Rmaxint = min(-log(eps) / Z / ka, Rmax)
Uee, errUee = integrate.quad(lambda r: pi4 * r * r * calUrho(r, ka, Z, n, l, m) * rho(ka, Z, n, l, m, r),
Rmin, Rmaxint, limit = nmaxdiv, epsrel = eps)
if 'e' in mode:
Uee *= Ne * Ne
else:
Uee *= Ne
return Uee, errUee
# UXa = -3.0 * alpha * (3/4pi*rho(r))^(1/3)
def calLocalUXa(r, ka, Z, n, l, m, Ne):
return -3.0 * alpha * pow(3.0/pi4 * rho(ka, Z, n, l, m, r), 1.0/3.0)
# UXa = -3.0 * alpha * integ(4pi * r * r * (3/4pi*rho(r))^(1/3) * rho(r)))
def calUXa(mode, ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps):
Rmaxint = min(-log(eps) / Z / ka, Rmax)
UXa, errUXa = integrate.quad(lambda r: pi4 * r * r * calLocalUXa(r, ka, Z, n, l, m, Ne) * rho(ka, Z, n, l, m, r),
Rmin, Rmaxint, limit = nmaxdiv, epsrel = eps)
if 'e' in mode:
UXa *= pow(Ne, 4.0/3.0)
else:
UXa *= pow(Ne, 1.0/3.0)
return UXa, errUXa
def calTotalEnergy(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps):
build_Qr(ka, Z, n, l, m)
#def calT(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps):
T, errT = calT(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
UeZ, errUeZ = calUeZ(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
Uee, errUee = calUee(mode, ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
UXa, errUXa = calUXa(mode, ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
Etot = T + UeZ + Uee + UXa
return T, UeZ, Uee, UXa, Etot
def calTotalEnergyOnly(kav, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps):
build_Qr(kav, Z, n, l, m)
T, errT = calT(kav, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
UeZ, errUeZ = calUeZ(kav, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
Uee, errUee = calUee('e', kav, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
UXa, errUXa = calUXa('e', kav, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
Etot = T + UeZ + Uee + UXa
return Etot
def calOptimizedTotalEnergy(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps):
xa = [ka]
ret = minimize(lambda xa: calTotalEnergyOnly(xa[0], Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps),
xa, method = method, jac = diff1, tol = tol,
callback = lambda xa: callback(xa),
options = {'maxiter':maxiter, "disp":True})
# print("ret=", ret)
if method == 'nelder-mead':
simplex = ret['final_simplex']
ai = simplex[0][0]
Emin = ret['fun']
elif method == 'cg':
ai = ret['x']
Emin = ret['fun']
elif method == 'powell':
ai = ret['x']
Emin = ret['fun']
elif method == 'bfgs':
ai = ret['x']
ka = xa[0]
Emin = calTotalEnergyOnly(xa[0], Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
ka = ai[0]
T, UeZ, Uee, UXa, Etot = calTotalEnergy(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
return T, UeZ, Uee, UXa, Etot, ka
# First derivatives to be used e.g. for cg method
# Approximate by forward difference method with the delta h = h_diff
def diff1(ai):
global Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps
n = len(ai)
f0 = Emin = calTotalEnergyOnly(ai[0], Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
df = np.empty(n)
for i in range(n):
aii = ai
aii[i] = ai[i] + h_diff
f1 = calTotalEnergyOnly(aii[0], Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
df[i] = (f1 - f0) / h_diff
return df
# Callback function for scipy.optimize.minimize()
# Print variables every iteration, and update graph for every graphupdateinterval iterationsおt
iter = 0
def callback(xk):
global iter
global Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps
ka = xk[0]
Etot = calTotalEnergyOnly(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
# パラメータと残差二乗和を表示
print("callback {}: ka={:14.4g} Emin={} eV".format(iter, ka, Etot * HartreeToeV))
iter += 1
def sweep_Ne(Eanal):
global Rmin, Rstep, nR, Rmaxdata, r
global ka
global qfunc
print("")
print("Not optimized")
print(" Parabolic expantion around Ne = 0.5")
Tp, UeZp, Ueep, UXap, Etotp = calTotalEnergy(ka, Z, n, l, m, 0.5 + hparab, Rmin, Rmax, nmaxdiv, eps)
T0, UeZ0, Uee0, UXa0, Etot0 = calTotalEnergy(ka, Z, n, l, m, 0.5 , Rmin, Rmax, nmaxdiv, eps)
Tm, UeZm, Ueem, UXam, Etotm = calTotalEnergy(ka, Z, n, l, m, 0.5 - hparab, Rmin, Rmax, nmaxdiv, eps)
Etotp *= HartreeToeV
Etot0 *= HartreeToeV
Etotm *= HartreeToeV
print(" Ne={}: E={} eV".format(0.5 + hparab, Etotp))
print(" Ne={}: E={} eV".format(0.5 , Etot0))
print(" Ne={}: E={} eV".format(0.5 - hparab, Etotm))
a2 = (Etotp - 2.0 * Etot0 + Etotm) / hparab / hparab
a1 = (Etotp - Etotm) / 2.0 / hparab
print(" E = {} + {} * Ne + {} * Ne^2".format(Etot0, a1, a2))
xNe = []
yE1s = []
yE1sparab = []
print("")
print("{:6s}\t{:6s}\t{:6s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}"
.format('ka', 'Z', 'Ne', 'T in eV', 'U(e-Z)', 'U(e-e)', 'U(Xa)',
ELabel, ELabel + ' (parbolic)'))
for Ne in Nearray:
T, UeZ, Uee, UXa, Etot = calTotalEnergy(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
Eparab = Etot0 + a1 * (Ne - 0.5) + a2 * pow(Ne - 0.5, 2)
print("{:6.4f}\t{:6.4f}\t{:6.4f}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}"
.format(ka, Z, Ne,
T * HartreeToeV, UeZ * HartreeToeV, Uee * HartreeToeV, UXa * HartreeToeV,
Etot * HartreeToeV, Eparab))
xNe.append(Ne)
yE1s.append(Etot * HartreeToeV)
yE1sparab.append(Eparab)
if 'v' in mode:
yE1sOpt = []
yE1sOptparab = []
ykaOpt = []
print("")
print("Optimized for ka by variational principle")
print(" Parabolic expantion around Ne = 0.5")
Tp, UeZp, Ueep, UXap, Etotp, kap = calOptimizedTotalEnergy(ka, Z, n, l, m, 0.5 + hparab, Rmin, Rmax, nmaxdiv, eps)
T0, UeZ0, Uee0, UXa0, Etot0, ka0 = calOptimizedTotalEnergy(ka, Z, n, l, m, 0.5 , Rmin, Rmax, nmaxdiv, eps)
Tm, UeZm, Ueem, UXam, Etotm, kam = calOptimizedTotalEnergy(ka, Z, n, l, m, 0.5 - hparab, Rmin, Rmax, nmaxdiv, eps)
Etotp *= HartreeToeV
Etot0 *= HartreeToeV
Etotm *= HartreeToeV
print(" Ne={}: E={} eV".format(0.5 + hparab, Etotp))
print(" Ne={}: E={} eV".format(0.5 , Etot0))
print(" Ne={}: E={} eV".format(0.5 - hparab, Etotm))
a2 = (Etotp - 2.0 * Etot0 + Etotm) / hparab / hparab
a1 = (Etotp - Etotm) / 2.0 / hparab
print(" E = {} + {} * Ne + {} * Ne^2".format(Etot0, a1, a2))
print("{:6s}\t{:6s}\t{:6s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}"
.format('ka', 'Z', 'Ne', 'T in eV', 'U(e-Z)', 'U(e-e)', 'U(Xa)', ELabel, ELabel + ' (parabolic)'))
for Ne in Nearray:
T, UeZ, Uee, UXa, Etot, ka = calOptimizedTotalEnergy(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
Eparab = Etot0 + a1 * (Ne - 0.5) + a2 * pow(Ne - 0.5, 2)
print("{:6.4f}\t{:6.4f}\t{:6.4g}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}t{:10.6g}"
.format(ka, Z, Ne,
T * HartreeToeV, UeZ * HartreeToeV, Uee * HartreeToeV, UXa * HartreeToeV,
Etot * HartreeToeV, Eparab))
yE1sOpt.append(Etot * HartreeToeV)
yE1sOptparab.append(Eparab)
ykaOpt.append(ka)
#=============================
# Plot graphs
#=============================
if 'g' not in mode:
terminate()
fig = plt.figure(figsize = (12, 8))
ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
# ax3 = fig.add_subplot(2, 3, 3)
# ax4 = fig.add_subplot(2, 3, 4)
# ax5 = fig.add_subplot(2, 3, 5)
ax1.plot(xNe, yE1s, label = ELabel + ' (non-optimized)', color = 'black', linewidth = 1.5, marker = 'o', markersize = 1.0)
ax1.plot(xNe, yE1sparab, label = ELabel + ' (non-opt,parabolic)', color = 'black', linestyle = 'dashed', linewidth = 0.5)
if 'v' in mode:
ax1.plot(xNe, yE1sOpt, label = ELabel + ' (optimized)', color = 'red', linewidth = 1.5, marker = 'o', markersize = 1.0)
ax1.plot(xNe, yE1sOptparab, label = ELabel + ' (opt,parabolic)', color = 'red', linewidth = 0.5)
ax1.plot([min(xNe), max(xNe)], [Eanal, Eanal], color = 'red', linestyle = 'dashed')
ax1.plot([0.5, 0.5], [min(yE1s), max(yE1s)], color = 'red', linestyle = 'dashed')
ax1.set_xlabel("Ne")
ax1.set_ylabel(ELabel + " (eV)")
ax1.legend()
if 'v' in mode:
ax2.plot(xNe, ykaOpt, label = 'ka (optimized)', color = 'black', linewidth = 0.5, marker = 'o', markersize = 1.0)
ax2.plot([min(xNe), max(xNe)], [1.0, 1.0], color = 'red', linestyle = 'dashed')
if 'v' in mode:
ax2.plot([0.5, 0.5], [min(ykaOpt), max(ykaOpt)], color = 'red', linestyle = 'dashed')
ax2.set_xlabel("Ne")
ax2.set_ylabel("ka (optimized)")
ax2.legend()
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
def sweep_ka(Eanal):
global Rmin, Rstep, nR, Rmaxdata, r
global qfunc
global nmaxdic, eps
xka = []
yE1s = []
print("")
print("{:6s}\t{:6s}\t{:6s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}"
.format('ka', 'Z', 'Ne', 'T in eV', 'U(e-Z)', 'U(e-e)', 'U(Xa)', ELabel))
for kav in kaarray:
T, UeZ, Uee, UXa, Etot = calTotalEnergy(kav, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
print("{:6.4f}\t{:6.4f}\t{:6.4f}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}"
.format(kav, Z, Ne,
T * HartreeToeV, UeZ * HartreeToeV, Uee * HartreeToeV, UXa * HartreeToeV, Etot * HartreeToeV))
xka.append(kav)
yE1s.append(Etot * HartreeToeV)
#=============================
# Plot graphs
#=============================
if 'g' not in mode:
terminate()
fig = plt.figure(figsize = (12, 8))
ax1 = fig.add_subplot(2, 3, 1)
ax2 = fig.add_subplot(2, 3, 2)
ax3 = fig.add_subplot(2, 3, 3)
ax4 = fig.add_subplot(2, 3, 4)
ax5 = fig.add_subplot(2, 3, 5)
ax1.plot(xka, yE1s, label = ELabel, color = 'black', marker = 'o')
ax1.plot([min(xka), max(xka)], [Eanal, Eanal], color = 'red', linestyle = 'dashed')
ax1.set_xlabel("ka")
ax1.set_ylabel(ELabel + " (eV)")
ax1.legend()
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
def debug(Eanal):
global ka, Z, n, l, m, Ne
global Rmin, Rstep, nR, Rmaxdata, r
ka0, Z0 = ka, Z
print("")
print("{:6s}\t{:6s}\t{:6s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}"
.format('ka', 'Z', 'Ne', 'T in eV', 'U(e-Z)', 'U(e-e)', 'U(Xa)', ELabel))
T, UeZ, Uee, UXa, Etot = calTotalEnergy(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
print("{:6.4f}\t{:6.4f}\t{:6.4f}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}"
.format(ka, Z, Ne,
T * HartreeToeV, UeZ * HartreeToeV, Uee * HartreeToeV, UXa * HartreeToeV, Etot * HartreeToeV))
if 'v' in mode:
print("")
print("Optimized for ka by variational principle")
print("{:6s}\t{:6s}\t{:6s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}\t{:10s}"
.format('ka', 'Z', 'Ne', 'T in eV', 'U(e-Z)', 'U(e-e)', 'U(Xa)', ELabel))
T, UeZ, Uee, UXa, Etot, ka = calOptimizedTotalEnergy(ka, Z, n, l, m, Ne, Rmin, Rmax, nmaxdiv, eps)
print("{:6.4f}\t{:6.4f}\t{:6.4f}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}\t{:10.6g}"
.format(ka, Z, Ne,
T * HartreeToeV, UeZ * HartreeToeV, Uee * HartreeToeV, UXa * HartreeToeV, Etot * HartreeToeV))
#=============================
# Plot graphs
#=============================
if 'g' not in mode:
terminate()
build_Qr(ka0, Z, n, l, m)
ypotZ = [] # U(Z) = -Z/r
ypotZrho = [] # U(e-Z) for Z = 1
ypotXa = [] # Xa potential
ypotrho = [] # Electrostatic potential by rho(r)
for i in range(len(r)):
if r[i] == 0.0:
phi = 0.0
else:
phi, errpot = integrate.quad(lambda r: pi4 * r * rho(ka, Z, n, l, m, r),
Rmin, r[i], limit = nmaxdiv, epsrel = eps)
potZ = -Z / r[i]
ypotZ.append(calUZ(r[i], Z))
ypotZrho.append(-Z * Ne * phi)
ypotrho.append(Ne * calUrho(r[i], ka, Z, n, l, m))
ypotXa.append(calLocalUXa(r[i], ka, Z, n, l, m, 1.0))
fig = plt.figure(figsize = (12, 8))
ax1 = fig.add_subplot(2, 3, 1)
ax2 = fig.add_subplot(2, 3, 2)
ax3 = fig.add_subplot(2, 3, 3)
ax1.plot(r, yRr, label = 'Rr(r)', color = 'black')
ax1.set_xlim([Rmin, Rmax])
ax1.set_ylim([0, max(yRr)*1.1])
ax1.set_xlabel("r (bohr)")
ax1.set_ylabel("Rr(r)")
ax1.legend()
ax2.plot(r, yQr, label = 'Q(r)', color = 'black')
ax2.set_xlabel("r (bohr)")
ax2.set_ylabel("Q(r)")
ax2.legend()
ax3.plot(r, ypotZ, label = 'U(Z)', color = 'black')
ax3.plot(r, ypotZrho, label = 'U(Z-rho)', color = 'red')
ax3.plot(r, -np.array(ypotrho), label = '-U(rho)', color = 'blue')
ax3.plot(r, ypotXa, label = 'U(Xa)', color = 'green')
ax3.set_ylim([min(ypotXa) * 5.0, 0.0])
ax3.set_xlabel("r (bohr)")
ax3.set_ylabel("Potential / Energy (Hartree)")
ax3.legend()
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
#======================
# main
#======================
def main():
global mode
global ka, Z, n, l, m, Ne
global Rmin, Rstep, nR, Rmaxdata, r
global qfunc
updatevars()
Rstep = (Rmax - Rmin) / (nR - 1)
r = [Rmin + i * Rstep for i in range(nR+100)]
Rmaxdata = max(r)
print("")
print("mode: ", mode)
print("")
print("Orbital: ka={} Z={} n={} l={} m={}".format(ka, Z, n, l, m))
print("Ne: ", Ne)
print("Integration: Rmax=", Rmax)
print(" Rmax: epsR={} Rmaxinteg={}".format(epsR, -log(epsR) / Z / ka))
print("")
print("Analytical solution")
Tanal = calTanal(Z, ka)
Uanal = calUanal(Z, ka)
Eanal = Tanal + Uanal
print("T(analytical) = {} eV".format(Tanal))
print("U(analytical) = {} eV".format(Uanal))
print(" Etotl(analytical) = {} eV".format(Eanal))
print("")
print("Numerical integration")
Rr2tot, err = integrate.quad(lambda r: r * r * rho(ka, Z, n, l, m, r), Rmin, Rmax, limit = nmaxdiv, epsrel = eps)
Rr2tot *= pi4
print("R(r) normalization check: 2pi * integ(r*r * Rr*2)dr = ", Rr2tot)
if 'd' in mode:
debug(Eanal)
if 'k' in mode:
sweep_ka(Eanal)
if 'n' in mode:
sweep_Ne(Eanal)
terminate()
if __name__ == '__main__':
usage()
main()