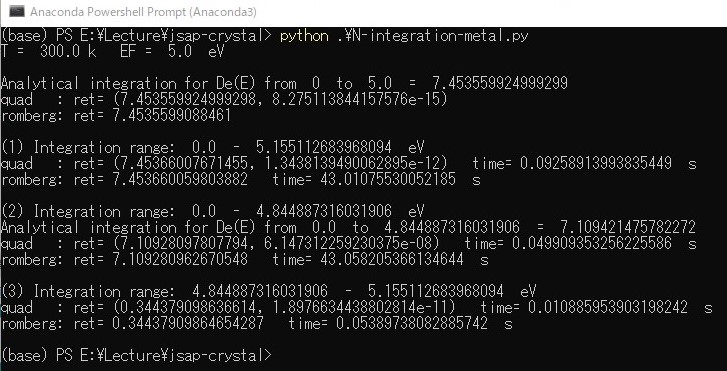
金属の有限温度 T における電子密度 N の計算。
数値積分の制度の確認
Download script from .\N-integration-metal.py
import sys
import time
from math import exp, sqrt
import numpy as np
from scipy import integrate # 数値積分関数 integrateを読み込む
from matplotlib import pyplot as plt
"""
金属の有限温度 T における電子密度 N の計算。
数値積分の制度の確認
"""
#定数
pi = 3.14159265358979323846
h = 6.6260755e-34 # Js";
hbar = 1.05459e-34 # "Js";
c = 2.99792458e8 # m/s";
e = 1.60218e-19 # C";
kB = 1.380658e-23 # JK-1";
# Temperature
T = 300.0 # K
# Fermi energy
EF = 5.0 # eV
# EF近傍の nrange * kBTの範囲で積分
nrange = 6.0
# quad/romberg積分の相対積分精度、quad関数のGauss積分の最大次数/romberg積分の最大分割数
eps = 1.0e-8
maxorder = 100
#計算時間を計測する繰り返し数
ncycle = 300
# Treat argments
argv = sys.argv
if len(argv) >= 2:
T = float(argv[1])
if len(argv) >= 3:
EF = float(argv[2])
ekBT = e / (kB * T) # eV単位のエネルギーを E/(kBT) に変換する係数
dE = nrange * kB * T / e
# 状態密度関数
def De(E):
return sqrt(E)
# FE分布関数
def fe(E, T, EF):
global kBT
if T == 0.0:
if E < EF:
return 1.0
else:
return 0.0
return 1.0 / (exp((E - EF) * ekBT) + 1.0)
# 被積分関数を定義
def Defe(E, T, EF):
return De(E) * fe(E, T, EF)
def main():
print("T = ", T, "k EF = ", EF, " eV")
print("")
Ianaly = 2.0 / 3.0 * pow(EF, 1.5)
print("Analytical integration for De(E) from ", 0, " to ", EF, " = ", Ianaly)
ret = integrate.quad(De, 0.0, EF, epsrel = eps)
print("quad : ret=", ret)
ret = integrate.romberg(De, 0.0, EF, rtol = eps, divmax = maxorder)
print("romberg: ret=", ret)
print("")
# 積分範囲
(Emin, Emax) = (0.0, EF + dE)
print("(1) Integration range: ", Emin, " - ", Emax, " eV")
t0 = time.time()
for i in range(ncycle):
ret = integrate.quad(lambda E: Defe(E, T, EF), Emin, Emax, epsrel = eps)
dt = time.time() - t0
print("quad : ret=", ret, " time=", dt, " s")
t0 = time.time()
for i in range(ncycle):
ret = integrate.romberg(lambda E: Defe(E, T, EF), Emin, Emax, rtol = eps, divmax = maxorder)
dt = time.time() - t0
print("romberg: ret=", ret, " time=", dt, " s")
print("")
# 積分範囲
(Emin, Emax) = (0.0, EF - dE)
print("(2) Integration range: ", Emin, " - ", Emax, " eV")
Ianaly = 2.0 / 3.0 * (pow(Emax, 1.5) - pow(Emin, 1.5))
print("Analytical integration for De(E) from ", Emin, " to ", Emax, " = ", Ianaly)
t0 = time.time()
for i in range(ncycle):
ret = integrate.quad(lambda E: Defe(E, T, EF), Emin, Emax, epsrel = eps)
dt = time.time() - t0
print("quad : ret=", ret, " time=", dt, " s")
t0 = time.time()
for i in range(ncycle):
ret = integrate.romberg(lambda E: Defe(E, T, EF), Emin, Emax, rtol = eps, divmax = maxorder)
dt = time.time() - t0
print("romberg: ret=", ret, " time=", dt, " s")
print("")
# 積分範囲
(Emin, Emax) = (EF - dE, EF + dE)
print("(3) Integration range: ", Emin, " - ", Emax, " eV")
t0 = time.time()
for i in range(ncycle):
ret = integrate.quad(lambda E: Defe(E, T, EF), Emin, Emax, epsrel = eps)
dt = time.time() - t0
print("quad : ret=", ret, " time=", dt, " s")
t0 = time.time()
for i in range(ncycle):
ret = integrate.romberg(lambda E: Defe(E, T, EF), Emin, Emax, rtol = eps, divmax = maxorder)
dt = time.time() - t0
print("romberg: ret=", ret, " time=", dt, " s")
print("")
if __name__ == '__main__':
main()