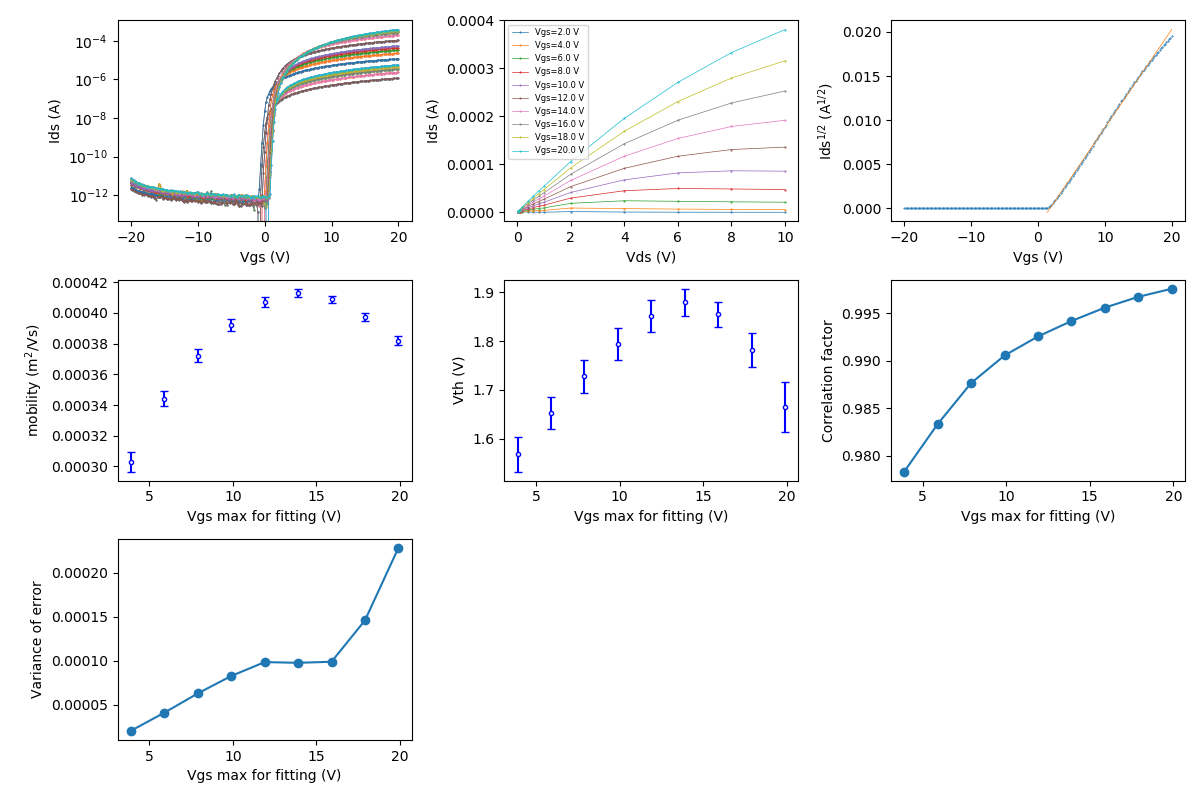
Estimate saturation mobility from TFT data
1st-order polynomial LSQ with error estimation
Download script from TFTiv_errorcheck.py
import sys
import re
import numpy as np
from numpy import sqrt, exp, sin, cos, tan, pi
import numpy.linalg as LA
import csv
from matplotlib import pyplot as plt
"""
Estimate saturation mobility from TFT data
1st-order polynomial LSQ with error estimation
"""
#===================================
# physical constants
#===================================
pi = 3.14159265358979323846
pi2 = 2.0 * pi
h = 6.6260755e-34 # Js";
hbar = 1.05459e-34 # "Js";
c = 2.99792458e8 # m/s";
e = 1.60218e-19 # C";
e0 = 8.854418782e-12; # C2N-1m-2";
kB = 1.380658e-23 # JK-1";
me = 9.1093897e-31 # kg";
R = 8.314462618 # J/K/mol
a0 = 5.29177e-11 # m";
#===================================
# parameters
#===================================
infile = 'TransferCurve.csv'
dg = 100.0e-9 # m
erg = 11.9
W = 300.0e-6 # m
L = 50.0e-6
Vds0 = 10.0 # V
xfitmin = 1.90 # V
xfitmax = 10.0
#===================================
# figure configuration
#===================================
fontsize = 12
legend_fontsize = 6
#==============================================
# fundamental functions
#==============================================
# 余計な文字が含まれている文字列から、
# 浮動小数点に変換できる最初の文字列を切り出し、
# 浮動小数点に変換して返す
def pfloat(str, defval = None):
# 文字列から、浮動小数点に使える文字が連続している部分を切り出す
if type(str) is float:
return str
m = re.search(r'([+\-eE\d\.]+)', str)
# print("str, m=", str, m)
# 一致した文字列を取得
valstr = m.group()
try:
return float(valstr)
except:
return defval
# pfloat()のint版
def pint(str):
try:
return int(str)
except:
return None
# 起動時引数を取得するsys.argリスト変数は、範囲外のindexを渡すとエラーになってプログラムが終了する
# egtarg()では、範囲外のindexを渡したときは、defvalを返す
def getarg(position, defval = None):
try:
return sys.argv[position]
except:
return defval
# 起動時引数を実数に変換して返す
def getfloatarg(position, defval = None):
return pfloat(getarg(position, defval))
# 起動時引数を整数値に変換して返す
def getintarg(position, defval = None):
return pint(getarg(position, defval))
def usage():
print("")
print("Usage:")
print(" python {} (Vds0 xfitmax xfitmax)".format(sys.argv[0]))
def terminate():
print("")
usage()
exit()
#==============================================
# update default values by startup arguments
#==============================================
argv = sys.argv
#if len(argv) <= 1:
# print("")
# usage()
# print("")
# exit()
if len(argv) >= 2:
Vds0 = float(argv[1])
if len(argv) >= 3:
xfitmin = float(argv[2])
if len(argv) >= 4:
xfitmax = float(argv[3])
Vds0 = getfloatarg(1, Vds0)
xfitmin = getfloatarg(2, xfitmin)
xfitmax = getfloatarg(3, xfitmax)
#==============================================
# other functions
#==============================================
def savecsv(outfile, header, datalist):
try:
print("Write to [{}]".format(outfile))
f = open(outfile, 'w')
except:
# except IOError:
print("Error: Can not write to [{}]".format(outfile))
else:
fout = csv.writer(f, lineterminator='\n')
fout.writerow(header)
# fout.writerows(data)
for i in range(0, len(datalist[0])):
a = []
for j in range(len(datalist)):
a.append(datalist[j][i])
fout.writerow(a)
f.close()
def read_csv(fname):
print("")
with open(fname) as f:
fin = csv.reader(f)
labels = next(fin)
xlabel = labels[0]
# label行が 空文字 の場合、データとしては読み込まない
ylabels = []
for i in range(1, len(labels)):
if labels[i] == '':
break
ylabels.append(labels[i])
ny = len(ylabels)
# print("xlabel: ", xlabel)
# print("ylabels: ", ylabels)
# print("ny=", ny)
x = []
ylist = []
for i in range(ny):
ylist.append([])
for row in fin:
x.append(pfloat(row[0]))
for i in range(1, ny+1):
v = pfloat(row[i])
if v is not None:
ylist[i-1].append(v)
else:
ylist[i-1].append(None)
return xlabel, ylabels, x, ylist
# 誤差、相関係数計算付き 一次多項式線形最小二乗
def lsq1(x, y, iPrint = 0):
n = len(x)
sx = sum(x)
avx = sx / n
sy = sum(y)
avy = sy / n
sxx = sum([x[i] * x[i] for i in range(n)])
avxx = sxx /n
sxy = sum([x[i] * y[i] for i in range(n)])
avxy = sxy /n
syy = sum([y[i] * y[i] for i in range(n)])
avyy = syy /n
delta = n * sxx - sx * sx
b = (n * sxy - sx * sy) / delta
a = avy - b * avx
sum_ei2 = sum([pow(y[i] - a - b * x[i], 2) for i in range(n)])
sigma_ei = sqrt(sum_ei2 / (n - 1))
sigma_y2 = avyy - avy * avy - pow(avxy - avx * avy, 2) / (avxx - avx * avx)
sigma_y = sqrt(sigma_y2)
Sa = sigma_y * sqrt(avxx) / sqrt((n - 2) * (avxx - avx * avx))
Sb = sigma_y / sqrt((n - 2) * (avxx - avx * avx))
r = sxy / sqrt(sxx * syy)
if iPrint:
print("")
print("lsq1:")
print("n = ", n)
print("sx (average) = {:12.6g} ({:12.6g})".format(sx, avx))
print("sy (average) = {:12.6g} ({:12.6g})".format(sy, avy))
print("sxx (average) = {:12.6g} ({:12.6g})".format(sxx, avxx))
print("sxy (average) = {:12.6g} ({:12.6g})".format(sxy, avxy))
print("syy (average) = {:12.6g} ({:12.6g})".format(syy, avyy))
print("sum(ei^2) (average) = {:12.6g} ({:12.6g})".format(sum_ei2, sigma_ei))
print("sigma_y^2 = ", sigma_y2)
print("r = ", r)
print("")
print("a = {:12.6g} Sa = {:12.6g}".format(a, Sa))
print("b = {:12.6g} Sb = {:12.6g}".format(b, Sb))
print("")
res = {'sx': sx, 'sy': sy, 'sxx': sxx, 'sxy': sxy, 'syy': syy,
'Sa': Sa, 'Sb': Sb, 'r': r, 'sigma_ei': sigma_ei, 'residual': sum_ei2}
return a, b, res
def findindex(x, val, defval = None):
for i in range(len(x)):
if val - 1.0e-5 <= x[i]:
return i
return defval
def main():
global Vgs0
global xfitmin, xfitmax
Cox = erg * e0 / dg #(F/m^2)
print("")
print("Cox = {:12.6g} [F/m^2]".format(Cox))
xlabel, ylabels, Vgs, IdsVgs = read_csv(infile)
nVgs = len(IdsVgs[0])
nVds = len(ylabels)
Vds = []
for i in range(nVds):
Vds.append(pfloat(ylabels[i]))
print("")
print("nVds=", nVds)
print("nVgs=", nVgs)
print("xlabel : ", xlabel)
print("ylabels: ", ylabels)
print("Vds: ", Vds)
# for i in range(len(Idslist)):
# print("")
# print("Idslist[{}]: {}".format(i, Idslist[i]))
# 出力特性 Ids - Vds をプロットするためのデータを作る
IdsVds = np.empty([nVgs, nVds])
for ig in range(nVgs):
for id in range(nVds):
IdsVds[ig][id] = IdsVgs[id][ig]
# sqrt(Ids) - Vgsプロットをする Vds0 のデータ番号 iVds を探す
# Vds[i] が小さい方から順に、Vds0 <= Vds[i] となる i を探すが、
# 浮動小数点誤差があることを考慮し、Vds0 - 1.0e-3 <= Vds[i] とする
for i in range(nVds):
if Vds0 - 1.0e-3 <= Vds[i]:
iVds = i
break
# sqrt(Ids) データを作る
print("")
print("Vds used: {} V (iVds = {})".format(Vds[iVds], iVds))
sqrtIds = []
for ig in range(nVgs):
sqrtIds.append(sqrt(IdsVgs[iVds][ig]))
# print("sqrtIds=",sqrtIds)
# 最小二乗法のデータ
xfitall = []
yfitall = []
for i in range(nVgs):
xfitall.append(Vgs[i])
yfitall.append(sqrtIds[i])
# フィッティング結果の範囲依存性を確認
print("")
print("=== Check the effect of fitting range ===")
xecheck = [x for x in np.arange(xfitmin + 2.0, max(Vgs), 2.0)]
ymu = []
yVth = []
ySmu = []
ySVth = []
yr = []
ysigma = []
for xfitmax1 in xecheck:
# xfitmin/maxに対応するindexを求める
ixfitmin = findindex(xfitall, xfitmin, None)
ixfitmax = findindex(xfitall, xfitmax1, max(xfitall))
print("")
print("x range: {} - {} V".format(xfitmin, xfitmax1))
print(" index {} - {}".format(ixfitmin, ixfitmax))
ai = lsq1(xfitall[ixfitmin:ixfitmax+1], yfitall[ixfitmin:ixfitmax+1], 0)
res = ai[2]
residual = res['residual']
sigma_ei = res['sigma_ei']
Sa = res['Sa']
Sb = res['Sb']
r = res['r']
Vth = -ai[0] / ai[1]
grad = ai[1]
mu = grad * grad / (W * Cox / 2.0 / L)
SVth = sqrt(pow(Sa / ai[1], 2) + pow(Sb * ai[0] / ai[1] / ai[1], 2))
Smu = 2.0 * mu * Sb / ai[1]
yVth.append(Vth)
ymu.append(mu)
ySVth.append(SVth)
ySmu.append(Smu)
yr.append(r)
ysigma.append(sigma_ei)
print(" residual = {:8.6g}".format(residual))
print(" sqrt(residual/(n-1)) = {:8.6g}".format(sigma_ei))
print(" r = {:8.6g}".format(r))
print(" Vth = {:6.4g} (+-{:12.4g}) V".format(Vth, SVth))
print(" mu_sat = {:12.4g} (+-{:8.4g}) cm^2/Vs".format(1.0e4 * mu, 1.0e4 * Smu))
#与えられたフィッティング範囲で最小二乗を行い、グラフにプロットする
print("")
print("=== Fitting by the given fitting range ===")
# xfitmin/maxに対応するindexを求める
ixfitmin = findindex(xfitall, xfitmin, None)
ixfitmax = findindex(xfitall, xfitmax, max(xfitall))
xfit = xfitall[ixfitmin:ixfitmax+1]
yfit = yfitall[ixfitmin:ixfitmax+1]
print("")
print("Least squares fitting:")
print("Vgs range: {} - {} V".format(xfitmin, xfitmax))
print(" index {} - {}".format(ixfitmin, ixfitmax))
print("Vgs=", xfit)
print("Igs^(1/2)=", yfit)
ai = lsq1(xfit, yfit, 0)
res = ai[2]
Sa = res['Sa']
Sb = res['Sb']
r = res['r']
Vth = -ai[0] / ai[1]
grad = ai[1]
mu = grad * grad / (W * Cox / 2.0 / L)
#dVth = dVth/da * da + dVth/db * db = -1/a1 * da - a0/a1^2 * db
#SVth = sqrt((Sa/a1)^2 + (Sb * a0/a1^2)^2)
SVth = sqrt(pow(Sa / ai[1], 2) + pow(Sb * ai[0] / ai[1] / ai[1], 2))
#dmu = 2.0 * a1 * da1 / (W * Cox / 2 / L) = 2.0 * mu * da1 / a1
Smu = 2.0 * mu * Sb / ai[1]
print("")
print("y = a + bx")
print(" a = {:12.6g} (+-{:12.4g})".format(ai[0], Sa))
print(" b = {:12.6g} (+-{:12.4g})".format(ai[1], Sb))
print(" r = {:8.6g}".format(r))
print("")
print("Vth = {:6.4g} (+-{:12.4g}) V".format(Vth, SVth))
print("dIgs^1/2/dVgs = {:12.4g} (+-{:12.4g})A^(1/2)/V".format(grad, Sb))
print("mu_sat = {:12.4g} (+-{:8.4g}) m^2/Vs = {:12.4g} (+-{:8.4g}) cm^2/Vs"
.format(mu, Smu, 1.0e4 * mu, 1.0e4 * Smu))
xcal = []
ycal = []
xx = xfitmin - 0.5
xcal.append(xx)
ycal.append(ai[0] + ai[1] * xx)
xx = max(Vgs)
xcal.append(xx)
ycal.append(ai[0] + ai[1] * xx)
print("")
print("plot")
fig = plt.figure(figsize = (12, 8))
ax1 = fig.add_subplot(3, 3, 1)
ax2 = fig.add_subplot(3, 3, 2)
ax3 = fig.add_subplot(3, 3, 3)
ax4 = fig.add_subplot(3, 3, 4)
ax5 = fig.add_subplot(3, 3, 5)
ax6 = fig.add_subplot(3, 3, 6)
ax7 = fig.add_subplot(3, 3, 7)
# 伝達特性 Ids-Vgs のグラフ
for id in range(nVds):
ax1.plot(Vgs, IdsVgs[id], linewidth = 0.5, marker = 'o', markersize = 0.5,
label = 'Vds={} V'.format(Vds[id]))
for id in range(nVds):
ax1.plot(Vgs, IdsVgs[id], linewidth = 0.5, marker = 'o', markersize = 0.5,
label = 'Vds={} V'.format(Vds[id]))
ax1.set_xlabel('Vgs (V)')
ax1.set_ylabel("Ids (A)")
ax1.set_yscale('log')
# ax1.set_xlim([-0.5, 0.5])
# ax1.set_ylim([0.0, 0.5])
# ax1.legend(loc = 'upper left', fontsize = legend_fontsize)
# 出力特性 Ids-Vds のグラフ
# 20点の Vgs を選び、そのうち、線形でIdsが見えるデータのみ表示する
nskip = int(nVgs / 20.0 + 1.0e-6)
for ig in range(0, nVgs, nskip):
# 線形プロットで見えないほどIdsが小さいデータは表示しない
if max(IdsVds[ig]) < 1.0e-7:
continue
ax2.plot(Vds, IdsVds[ig], linewidth = 0.5, marker = 'o', markersize = 0.5,
label = 'Vgs={} V'.format(Vgs[ig]))
ax2.set_xlabel('Vds (V)')
ax2.set_ylabel("Ids (A)")
# ax2.set_xlim([-0.5, 0.5])
# ax2.set_ylim([0.0, 0.5])
ax2.legend(loc = 'upper left', fontsize = legend_fontsize)
# Ids^(1/2) - Vgs グラフ
ax3.plot(Vgs, sqrtIds, linestyle = 'none', marker = 'o', markersize = 0.5)
ax3.plot(xcal, ycal, linestyle = '-', linewidth = 0.5)
ax3.set_xlabel('Vgs (V)')
ax3.set_ylabel("Ids$^{1/2}$ (A$^{1/2}$)")
# ax2.set_xlim([-0.5, 0.5])
# ax2.set_ylim([0.0, 0.5])
# ax3.legend(loc = 'upper left', fontsize = legend_fontsize)
# 移動度−フィッティング範囲グラフ
ax4.errorbar(xecheck, ymu, yerr = ySmu,
capsize = 3.0, fmt = 'o', markersize = 3.0, ecolor = 'b', markeredgecolor = 'b', color = 'w')
ax4.set_xlabel("Vgs max for fitting (V)")
ax4.set_ylabel('mobility (m$^2$/Vs)')
# Vth−フィッティング範囲グラフ
ax5.errorbar(xecheck, yVth, yerr = ySVth,
capsize = 3.0, fmt = 'o', markersize = 3.0, ecolor = 'b', markeredgecolor = 'b', color = 'w')
ax5.set_xlabel("Vgs max for fitting (V)")
ax5.set_ylabel('Vth (V)')
# 相関係数−フィッティング範囲グラフ
ax6.plot(xecheck, yr, marker = 'o')
ax6.set_xlabel("Vgs max for fitting (V)")
ax6.set_ylabel('Correlation factor')
# 誤差の分散−フィッティング範囲グラフ
ax7.plot(xecheck, ysigma, marker = 'o')
ax7.set_xlabel("Vgs max for fitting (V)")
ax7.set_ylabel('Variance of error')
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
terminate()
if (__name__ == '__main__'):
main()