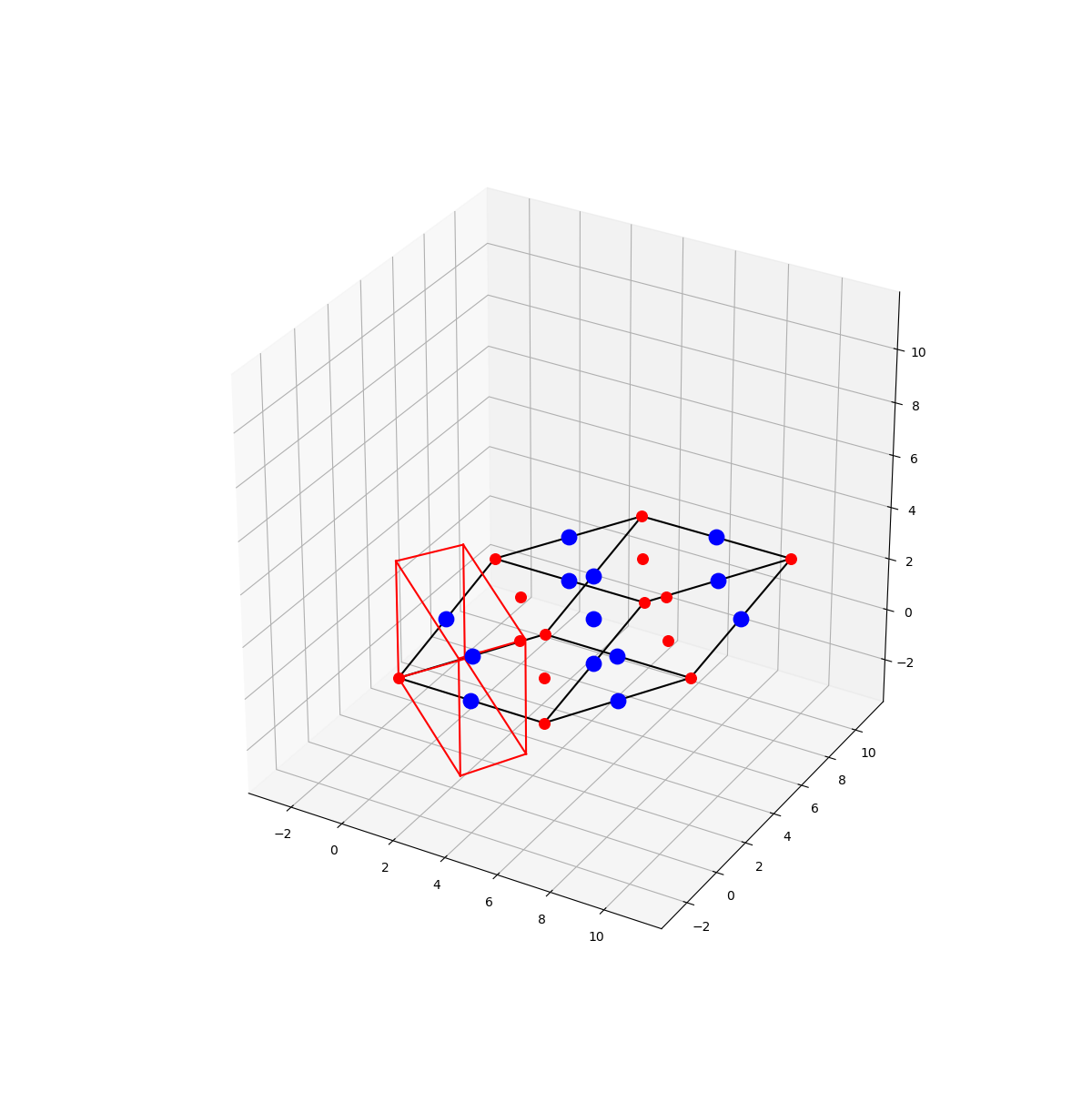
Draw unit cell and reciprocal unit cell
Requirement: tkcrystalbase.py
Download script from .\crystal_draw_cell.py
import sys
import os
import copy
from numpy import sin, cos, tan, arcsin, arccos, arctan, exp, log, sqrt
import numpy as np
from numpy import linalg as la
from tkcrystalbase import *
"""
Draw unit cell and reciprocal unit cell
Requirement: tkcrystalbase.py
"""
# Lattice parameters (angstrom and degree)
lattice_parameters = [ 5.62, 5.62, 5.62, 60.0, 60.0, 60.0]
#lattice_parameters = [ 5.62, 5.62, 5.62, 90.0, 90.0, 90.0]
# Site information (atom name, site label, atomic number, atomic mass, charge, radius, color, position)
sites = [
['Na', 'Na1', 11, 22.98997, +1.0, 0.7, 'red', np.array([0.0, 0.0, 0.0])]
,['Na', 'Na2', 11, 22.98997, +1.0, 0.7, 'red', np.array([0.0, 0.5, 0.5])]
,['Na', 'Na3', 11, 22.98997, +1.0, 0.7, 'red', np.array([0.5, 0.0, 0.5])]
,['Na', 'Na4', 11, 22.98997, +1.0, 0.7, 'red', np.array([0.5, 0.5, 0.0])]
,['Cl', 'Cl1', 17, 35.4527, -1.0, 1.4, 'blue', np.array([0.5, 0.0, 0.0])]
,['Cl', 'Cl2', 17, 35.4527, -1.0, 1.4, 'blue', np.array([0.5, 0.5, 0.5])]
,['Cl', 'Cl3', 17, 35.4527, -1.0, 1.4, 'blue', np.array([0.0, 0.0, 0.5])]
,['Cl', 'Cl4', 17, 35.4527, -1.0, 1.4, 'blue', np.array([0.0, 0.5, 0.0])]
]
# Coefficient for atomic size to plot
kr = 100.0
# Distance to judge identical atom site, in angstrom
rmin = 0.1
# Coefficient to plot reciprocal unit cell w.r.t. real space unit cell
kRUC = 0.8
# Range of unit cells to draw crystal structure
nrange = [[-0.1, 1.1], [-0.1, 1.1], [-0.1, 1.1]]
# Figure configuration
figsize = (12, 12)
def main():
print("")
print("Lattice parameters:", lattice_parameters)
aij = cal_lattice_vectors(lattice_parameters)
print("Lattice vectors:")
print(" ax: ({:10.4g}, {:10.4g}, {:10.4g}) A".format(aij[0][0], aij[0][1], aij[0][2]))
print(" ay: ({:10.4g}, {:10.4g}, {:10.4g}) A".format(aij[1][0], aij[1][1], aij[1][2]))
print(" az: ({:10.4g}, {:10.4g}, {:10.4g}) A".format(aij[2][0], aij[2][1], aij[2][2]))
inf = cal_metrics(lattice_parameters)
gij = inf['gij']
print("Metric tensor:")
print(" gij: ({:10.4g}, {:10.4g}, {:10.4g}) A".format(*gij[0]))
print(" ({:10.4g}, {:10.4g}, {:10.4g}) A".format(*gij[1]))
print(" ({:10.4g}, {:10.4g}, {:10.4g}) A".format(*gij[2]))
volume = cal_volume(aij)
print("Volume: {:12.4g} A^3".format(volume))
print("")
print("Unit cell volume: {:12.4g} A^3".format(volume))
Raij = cal_reciprocal_lattice_vectors(aij)
Rlatt = cal_reciprocal_lattice_parameters(Raij)
Rinf = cal_metrics(Rlatt)
Rgij = Rinf['gij']
print("Reciprocal lattice parameters:", Rlatt)
print("Reciprocal lattice vectors:")
print(" Rax: ({:10.4g}, {:10.4g}, {:10.4g}) A^-1".format(*Raij[0]))
print(" Ray: ({:10.4g}, {:10.4g}, {:10.4g}) A^-1".format(*Raij[1]))
print(" Raz: ({:10.4g}, {:10.4g}, {:10.4g}) A^-1".format(*Raij[2]))
print("Reciprocal lattice metric tensor:")
print(" Rgij: ({:10.4g}, {:10.4g}, {:10.4g}) A^-1".format(*Rgij[0]))
print(" ({:10.4g}, {:10.4g}, {:10.4g}) A^-1".format(*Rgij[1]))
print(" ({:10.4g}, {:10.4g}, {:10.4g}) A^-1".format(*Rgij[2]))
Rvolume = cal_volume(Raij)
print("Reciprocal unit cell volume: {:12.4g} A^-3".format(Rvolume))
allsites = []
for site in sites:
name, label, z, M, q, r, color, pos = copy.deepcopy(site)
pos01 = [reduce01(pos[0]), reduce01(pos[1]), reduce01(pos[2])]
for iz in range(int(nrange[2][0]) - 1, int(nrange[2][1]) + 1):
for iy in range(int(nrange[1][0]) - 1, int(nrange[1][1]) + 1):
for ix in range(int(nrange[0][0]) - 1, int(nrange[0][1]) + 1):
posn = [pos01[0] + ix, pos01[1] + iy, pos01[2] + iz]
if -0.1 <= posn[0] <= 1.1 and -0.1 <= posn[1] <= 1.1 and -0.1 <= posn[2] <= 1.1:
add_site(allsites, [name, label, z, M, q, r, color, posn], gij, rmin)
print("")
print("All sites to draw:")
for s in allsites:
print(" {:4}: {:4}: ({:8.3g}, {:8.3g}, {:8.3g}) Z={:6.3g}".format(s[0], s[1], s[7][0], s[7][1], s[7][2], s[4]))
fig = plt.figure(figsize = figsize)
ax = fig.add_subplot(111, projection='3d')
# Real space unit cell
draw_unitcell(ax, allsites, aij, nrange, kr, linecolor = 'black')
# Reciprocal space unit cell
k = max([*aij[0], *aij[1], *aij[2]]) / max([*Raij[0], *Raij[1], *Raij[2]]) * kRUC
kRaij = np.empty([3, 3])
for i in range(3):
for j in range(3):
kRaij[i][j] = k * Raij[i][j]
draw_unitcell(ax, None, kRaij, nrange, linecolor = 'red')
# Note: set_aspect() is not implemented for 3D plots
# ax.set_aspect('equal','box')
xlim =ax.get_xlim()
ylim =ax.get_ylim()
zlim =ax.get_zlim()
lim = [min([xlim[0], ylim[0], zlim[0]]), max([xlim[1], ylim[1], zlim[1]])]
ax.set_xlim(lim)
ax.set_ylim(lim)
ax.set_zlim(lim)
# ax.set_xticks(np.linspace(*lim, 0))
# ax.set_yticks(np.linspace(*lim, 0))
# ax.set_zticks(np.linspace(*lim, 0))
plt.show()
print("")
exit()
if __name__ == '__main__':
main()