1D band calculation by Kronig-Penney model
Download script from kronig_penney.py
import sys
import numpy as np
from numpy import sqrt, exp, sin, cos, tan, cosh, sinh
import numpy.linalg as LA
from pprint import pprint
import csv
from matplotlib import pyplot as plt
"""
1D band calculation by Kronig-Penney model
"""
#===================================
# physical constants
#===================================
pi = 3.14159265358979323846
pi2 = 2.0 * pi
h = 6.6260755e-34 # Js";
hbar = 1.05459e-34 # "Js";
c = 2.99792458e8 # m/s";
e = 1.60218e-19 # C";
e0 = 8.854418782e-12; # C2N-1m-2";
kB = 1.380658e-23 # JK-1";
me = 9.1093897e-31 # kg";
R = 8.314462618 # J/K/mol
a0 = 5.29177e-11 # m";
#========================
# global configuration
#========================
mode = 'graph' # graph|band|wf
#========================
# Crystal definition
#========================
# Si
a = 5.4064 # angstrom, lattice parameter
#========================
# Potential
#========================
bwidth = 0.5 # A, barrier width
bpot = 10.0 # eV, barrier height
#=====================================
# 解を走査するグラフ表示
#=====================================
kg = 0.0 # k point to be plotted
# 解を走査するエネルギー範囲
Emin = 0.0
Emax = 9.5
# グラフを表示するエネルギー点数
nE = 51
# 解を走査するエネルギー点数
nEsearch = nE
# Newton法パラメータ
eps = 1.0e-8
nmaxiter = 100
dump = 0.0
#========================
# Band
#========================
kmin = -0.5 # in pi/a
kmax = 0.5 # in pi/a
nk = 21
# プロットするエネルギー範囲
Erange = [0.0, 10.0] # eV
# リストに保存する準位最大数
nMaxLevel = 15
#========================
# Wave function
#========================
#波動関数を描画するx範囲
xwmin = 0.0 # A
xwmax = 3.0 * a # A
nxw = 101
#描画する波動関数の波数
kw = 0.0
#描画する波動関数の準位番号
iLevel = 0
#===================================
# figure configuration
#===================================
figsize = (6, 8)
fontsize = 12
legend_fontsize = 8
#==============================================
# fundamental functions
#==============================================
# 実数値に変換できない文字列をfloat()で変換するとエラーになってプログラムが終了する
# この関数は、変換できなかったらNoneを返すが、プログラムは終了させない
def pfloat(str):
try:
return float(str)
except:
return None
# pfloat()のint版
def pint(str):
try:
return int(str)
except:
return None
# 起動時引数を取得するsys.argリスト変数は、範囲外のindexを渡すとエラーになってプログラムが終了する
# egtarg()では、範囲外のindexを渡したときは、defvalを返す
def getarg(position, defval = None):
try:
return sys.argv[position]
except:
return defval
# 起動時引数を実数に変換して返す
def getfloatarg(position, defval = None):
return pfloat(getarg(position, defval))
# 起動時引数を整数値に変換して返す
def getintarg(position, defval = None):
return pint(getarg(position, defval))
# x を aで割った余り x0 と整数 n
def round01(x, a):
if x >= 0.0:
n = int(x / a)
else:
n = int(x / a) - 1
x0 = x - n * a
return x0, n
def usage():
print("")
print("Usage: Variables in () are optional")
print(" python {}".format(sys.argv[0]))
print(" python {} (graph a bwidth bpot k Emin Emax nE)".format(sys.argv[0]))
print(" python {} (band a bwidth bpot nG kmin kmax nk)".format(sys.argv[0]))
print(" python {} (wf a bwidth bpot kw iLevel xwmin xwmax nxw)".format(sys.argv[0]))
print(" ex: python {} {} {} {} {} {} {} {} {}"
.format(sys.argv[0], 'graph', a, bwidth, bpot, kg, Emin, Emax, nE))
print(" ex: python {} {} {} {} {} {} {} {}"
.format(sys.argv[0], 'band', a, bwidth, bpot, kmin, kmax, nk))
print(" ex: python {} {} {} {} {} {} {} {} {} {}"
.format(sys.argv[0], 'wf', a, bwidth, bpot, kw, iLevel, xwmin, xwmax, nxw))
def terminate(message = None):
print("")
if message is not None:
print("")
print(message)
print("")
usage()
print("")
exit()
#==============================================
# update default values by startup arguments
#==============================================
argv = sys.argv
#if len(argv) == 1:
# terminate()
mode = getarg (1, mode)
a = getfloatarg(2, a)
bwidth = getfloatarg(3, bwidth)
bpot = getfloatarg(4, bpot)
if mode == 'graph':
kg = getfloatarg(5, kg)
Emin = getfloatarg(6, Emin)
Emax = getfloatarg(7, Emax)
nE = getintarg (8, nE)
elif mode == 'band':
kmin = getfloatarg( 5, kmin)
kmax = getfloatarg( 6, kmax)
nk = getintarg ( 7, nk)
elif mode == 'wf':
kw = getfloatarg( 5, kw)
iLevel = getintarg ( 6, iLevel)
xwmin = getfloatarg( 7, xwmin)
xwmax = getfloatarg( 8, xwmax)
nxw = getintarg (9, nxw)
# rectangular barrier potential
def pot(x):
global a
global bwidth, bpot
xred, nred = round01(x, a)
if a - bwidth <= xred < a:
return bpot
return 0.0
# ポテンシャルV(x)のリストを返す
def build_potential(xmin, xstep, n):
xpot = np.empty(n)
ypot = np.empty(n)
for i in range(n):
xx = xmin + i * xstep
xpot[i] = xx
ypot[i] = pot(xx)
return xpot, ypot
# Kronig-Penneyモデルの方程式の誤差
def cal_delta(E, k, w, b, V0):
alpha = sqrt(2.0 * me * E * e) / hbar
beta = sqrt(2.0 * me * (V0 - E) * e) / hbar
ka = k * pi2
alphaw = alpha * w * 1.0e-10
betab = beta * b * 1.0e-10
delta = (beta*beta - alpha*alpha)/2.0/alpha/beta * sin(alphaw) * sinh(betab) \
+ cos(alphaw) * cosh(betab) \
- cos(ka)
# print("a=", E, ka, alphaw, betab, delta)
return delta
# ciがKronig-Penneyモデルの方程式を満たすかどうかを確認
# デバッグ用
def check_ci(ci, kw, Ei, w, b, V0, eps, IsPrint = 0):
alpha = sqrt(2.0 * me * Ei * e) / hbar
beta = sqrt(2.0 * me * (V0 - Ei) * e) / hbar
ka = kw * pi2
lambda_ = exp(1.0j * ka)
alphaw = alpha * w * 1.0e-10
betab = beta * b * 1.0e-10
alpha *= 1.0e-10
beta *= 1.0e-10
Passed = 1
vmax = 0.0
if 1:
Mij = np.empty([4, 4], dtype = complex)
M3ij = np.empty([3, 3], dtype = complex)
V3i = np.empty([3, 1], dtype = complex)
Mij[0, 0] = Mij[0, 1] = 1.0
Mij[0, 2] = Mij[0, 3] = -1.0
Mij[1, 0] = 1.0j * alpha
Mij[1, 1] = -1.0j * alpha
Mij[1, 2] = -beta
Mij[1, 3] = beta
Mij[2, 0] = exp( 1.0j * alphaw)
Mij[2, 1] = exp(-1.0j * alphaw)
Mij[2, 2] = -lambda_ * exp(-betab)
Mij[2, 3] = -lambda_ * exp( betab)
Mij[3, 0] = 1.0j * alpha * exp( 1.0j * alphaw)
Mij[3, 1] = -1.0j * alpha * exp(-1.0j * alphaw)
Mij[3, 2] = -lambda_ * beta * exp(-betab)
Mij[3, 3] = lambda_ * beta * exp( betab)
if IsPrint:
for i in range(4):
print(" ci[{}] = {:12.4g}+j{:12.4g}".format(i, ci[i].real, ci[i].imag))
for i in range(4):
v = Mij[i, 0] * ci[0] + Mij[i, 1] * ci[1] + Mij[i, 2] * ci[2] + Mij[i, 3] * ci[3]
v = abs(v)
if IsPrint:
print(" abs(Mij@ci[{}]) = {}".format(i, v), eps)
if v > eps:
Passed = 0
if v > vmax:
vmax = v
if not Passed:
print("Error: Mij @ ci is not zero: abs(Mij@ci)={} > eps={}".format(vmax, eps))
exit()
def refine_E(E0, E1, nmaxiter, eps, dump, k, w, b, V0, IsPrint = 0):
delta0 = cal_delta(E0, k, w, b, V0)
delta1 = cal_delta(E1, k, w, b, V0)
for i in range(nmaxiter):
diff = (delta1 - delta0) / (E1 - E0)
if diff >= 0.0:
diff += dump
else:
diff = -(abs(diff) + dump)
dE = -delta1 / diff
E2 = E1 + dE
delta2 = cal_delta(E2, k, w, b, V0)
if abs(dE) < eps:
if IsPrint:
print(" converged at E = {:12.6g} with dE = {:12.6g} delta = {:12.6g}"
.format(E2, dE, delta2))
return E2, dE, delta2
else:
E0 = E1
E1 = E2
delta0 = delta1
delta1 = delta2
continue
else:
print(" Not converged for {} iterations.".format(nmaxiter))
print(" E = {:12.6g} with dE = {:12.6g} delta = {:12.6g}".format(E2, dE, delta2))
return None, None, None
# delta(E)を走査し、delta(E)=0を満たすEのリストを返す
def find_Elist(Emin, Emax, nEsearch, k, w, b, V0):
# nEsearch *= 100
Estep = (Emax - Emin) / (nEsearch - 1)
# print("Estep=", Estep)
d0 = None
iband = 0
Elist = []
Alist = []
for iE in range(nEsearch):
E = Emin + iE * Estep
if E == 0.0:
continue
if V0 <= E:
break
delta = cal_delta(E, k, w, b, V0)
if d0 is None:
d0 = delta
continue
if d0 * delta < 0.0:
d0 = delta
# print(" E[{}]={:12.6g} eV delta={:8.4g}".format(iband, E, delta))
E, dE, delta0 = refine_E(E - Estep, E, nmaxiter, eps, dump, k, w, b, V0, IsPrint = 0)
print(" E[{}]={:12.6g} eV dE={:12.6g} delta={:12.6g}".format(iband, E, dE, delta0))
Elist.append(E)
# Elist.append(E - 0.5 * Estep)
alpha = sqrt(2.0 * me * E * e) / hbar
beta = sqrt(2.0 * me * (V0 - E) * e) / hbar
ka = k * pi2
lambda_ = exp(1.0j * ka)
alphaw = alpha * w * 1.0e-10
betab = beta * b * 1.0e-10
alpha *= 1.0e-10
beta *= 1.0e-10
Mij = np.empty([4, 4], dtype = complex)
M3ij = np.empty([3, 3], dtype = complex)
V3i = np.empty([3, 1], dtype = complex)
Mij[0, 0] = Mij[0, 1] = 1.0
Mij[0, 2] = Mij[0, 3] = -1.0
Mij[1, 0] = 1.0j * alpha
Mij[1, 1] = -1.0j * alpha
Mij[1, 2] = -beta
Mij[1, 3] = beta
Mij[2, 0] = exp( 1.0j * alphaw)
Mij[2, 1] = exp(-1.0j * alphaw)
Mij[2, 2] = -lambda_ * exp(-betab)
Mij[2, 3] = -lambda_ * exp( betab)
Mij[3, 0] = 1.0j * alpha * exp( 1.0j * alphaw)
Mij[3, 1] = -1.0j * alpha * exp(-1.0j * alphaw)
Mij[3, 2] = -lambda_ * beta * exp(-betab)
Mij[3, 3] = lambda_ * beta * exp( betab)
A = 1.0
M3ij[0, 0] = Mij[1, 1]
M3ij[0, 1] = Mij[1, 2]
M3ij[0, 2] = Mij[1, 3]
M3ij[1, 0] = Mij[2, 1]
M3ij[1, 1] = Mij[2, 2]
M3ij[1, 2] = Mij[2, 3]
M3ij[2, 0] = Mij[3, 1]
M3ij[2, 1] = Mij[3, 2]
M3ij[2, 2] = Mij[3, 3]
V3i[0, 0] = -A * Mij[1, 0]
V3i[1, 0] = -A * Mij[2, 0]
V3i[2, 0] = -A * Mij[3, 0]
Ai = LA.solve(M3ij, V3i)
ci = [A, Ai[0, 0], Ai[1, 0], Ai[2, 0]]
# check_ci(ci, k, E, w, b, V0, 3.0e-3, IsPrint = 0)
Alist.append(ci)
E += Estep
return Elist, Alist
# ciから、Ei(k)の波動関数を計算する
def cal_wavefunction(ci, x, kw, Ei, w, b, V0):
IsPrint = 1
a = w + b
xmin = -b
xmax = w
x0, n = round01(x, a)
if x0 < -xmin:
x0 += a
if x0 >= xmax:
x0 -= a
if not xmin <= x0 < xmax:
print("Error: x0 out of range: x={:8.4g} {} x0={:8.4g} w={:8.4g} b={:8.4g}".format(x, n, x0, w, b))
exit()
# if IsPrint:
# print("x={:8.4g} {} x0={:8.4g} w={:8.4g} b={:8.4g}".format(x, n, x0, w, b))
# check_ci(ci, kw, Ei, w, b, V0, 3.0e-3)
alpha = sqrt(2.0 * me * Ei * e) / hbar
beta = sqrt(2.0 * me * (V0 - Ei) * e) / hbar
alpha *= 1.0e-10
beta *= 1.0e-10
phase0 = pi2 / a * kw * x0
kph0 = exp(1.0j * phase0)
# Calculate the periodic function u(x) from phi(x) in -b <= x < w
if xmin <= x0 < 0.0: # in barrier, defined in -b <= x < 0, w <= x < a
f = ci[2] * exp(beta * x0) + ci[3] * exp(-beta * x0)
u = f / kph0
else: # in well, defined in 0 <= x < w
f = ci[0] * exp(1.0j * alpha * x0) + ci[1] * exp(-1.0j * alpha * x0)
u = f / kph0
# Calculate Bloch function phi(x) = exp(ikx) * u(x)
f = exp(1.0j * pi2 / a * kw * x) * u
return f + 0.0j
# デバッグ用: 周期関数部分 u(x) を返す
# return u + 0.0j
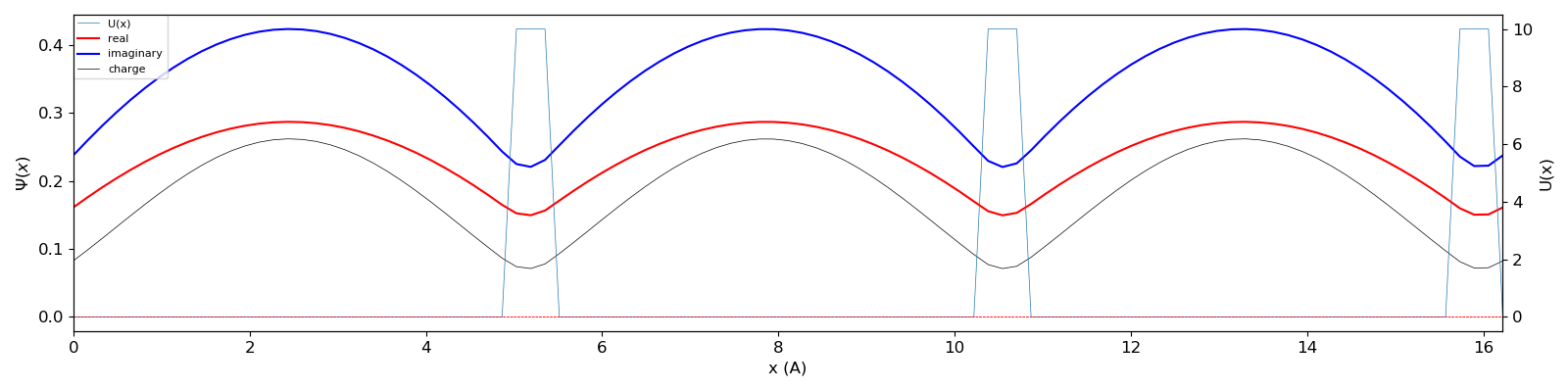
def wf():
global mode
global a
global bwidth, bpot
global nEsearch, nMaxLevel
global kw, iLevel
global xwmin, xwmax, nxw
xwstep = (xwmax - xwmin) / (nxw - 1)
Estep = bpot / (nEsearch - 1)
print("")
print("=== Input parameterss ===")
print("mode:", mode)
print("a=", a, "A")
print("Wave function to be plotted: k = {} iLevel = {}".format(kw, iLevel))
print("x range: {} - {} at {} step, {} points".format(xwmin, xwmax, xwstep, nxw))
print("potential: w={} A h={} eV".format(bwidth, bpot))
print("")
V0 = bpot
b = bwidth
w = a - b
print("")
print("at k={:8.4g}".format(kw))
Elist, Alist = find_Elist(0.0, V0, nEsearch, kw, w, b, V0)
xplot, yplot = build_potential(xwmin, xwstep, nxw)
print("")
print("=== Calculate wave function ===")
print("Energy levels:", Elist, "eV")
print("at k = {}".format(kw))
print("{}-th energy level".format(iLevel))
Ei = Elist[iLevel]
ci = Alist[iLevel]
print(" E = {:12.6g} eV".format(Elist[iLevel]))
print(" A = {:12.4g}+j{:12.4g}".format(ci[0].real, ci[0].imag))
print(" B = {:12.4g}+j{:12.4g}".format(ci[1].real, ci[1].imag))
print(" C = {:12.4g}+j{:12.4g}".format(ci[2].real, ci[2].imag))
print(" D = {:12.4g}+j{:12.4g}".format(ci[3].real, ci[3].imag))
sumci = abs(ci[0] + ci[1] - ci[2] - ci[3])
print(" sum(ci) = {:12.4e}".format(sumci))
alpha = sqrt(2.0 * me * Ei * e) / hbar * 1.0e-10
beta = sqrt(2.0 * me * (V0 - Ei) * e) / hbar * 1.0e-10
print(" alpha = {:12.6g} A^-1".format(alpha))
print(" beta = {:12.6g} A^-1".format(beta))
print("")
print("Normalization")
nxintg = int(a / xwstep + 1.0001)
xintgstep = a / (nxintg - 1)
chg = 0.0
for i in range(nxintg):
x = 0.0 + i * xintgstep
yval = cal_wavefunction(ci, x, kw, Ei, w, b, V0)
chg += yval * yval.conjugate()
chg = chg.real * xintgstep
kywf = 1.0 / sqrt(chg)
print("integ(|psi(x)|^2) = ", chg)
print("Normalization coefficient = ", kywf)
for i in range(4):
ci[i] *= kywf
print(" A = {:12.4g}+j{:12.4g}".format(ci[0].real, ci[0].imag))
print(" B = {:12.4g}+j{:12.4g}".format(ci[1].real, ci[1].imag))
print(" C = {:12.4g}+j{:12.4g}".format(ci[2].real, ci[2].imag))
print(" D = {:12.4g}+j{:12.4g}".format(ci[3].real, ci[3].imag))
ywf = np.empty(nxw, dtype = complex)
for i in range(nxw):
x = xwmin + i * xwstep
ywf[i] = cal_wavefunction(ci, x, kw, Ei, w, b, V0)
charge = [(ywf[i] * ywf[i].conjugate()).real for i in range(nxw)]
fig = plt.figure(figsize = (16, 4)) #figsize)
ax2 = fig.add_subplot(1, 1, 1)
# ax2 = fig.add_subplot(2, 1, 2)
ax1 = ax2.twinx()
ax1.set_xlim([xwmin, xwmax])
ax1.plot(xplot, yplot, linewidth = 0.5, label = 'U(x)')
ax1.plot(ax1.get_xlim(), [0.0, 0.0], color = 'r', linestyle = 'dashed', linewidth = 0.5)
ax2.set_xlim([xwmin, xwmax])
ax2.plot(xplot, ywf.real, color = 'r', linewidth = 1.5, label = "real")
ax2.plot(xplot, ywf.imag, color = 'b', linewidth = 1.5, label = "imaginary")
ax2.plot(xplot, charge, color = 'black', linewidth = 0.5, label = "charge")
ax2.plot(ax1.get_xlim(), [0.0, 0.0], color = 'r', linestyle = 'dashed', linewidth = 0.5)
ax1.set_xlabel("x (A)", fontsize = fontsize)
ax1.set_ylabel("U(x)", fontsize = fontsize)
ax2.set_xlabel("x (A)", fontsize = fontsize)
ax2.set_ylabel("$\Psi$($x$)", fontsize = fontsize)
handler1, label1 = ax1.get_legend_handles_labels()
handler2, label2 = ax2.get_legend_handles_labels()
ax2.legend(handler1 + handler2, label1 + label2, loc = 2, borderaxespad = 0.0, fontsize = legend_fontsize)
# ax2.legend(fontsize = legend_fontsize)
ax1.tick_params(labelsize = fontsize)
ax2.tick_params(labelsize = fontsize)
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
terminate()
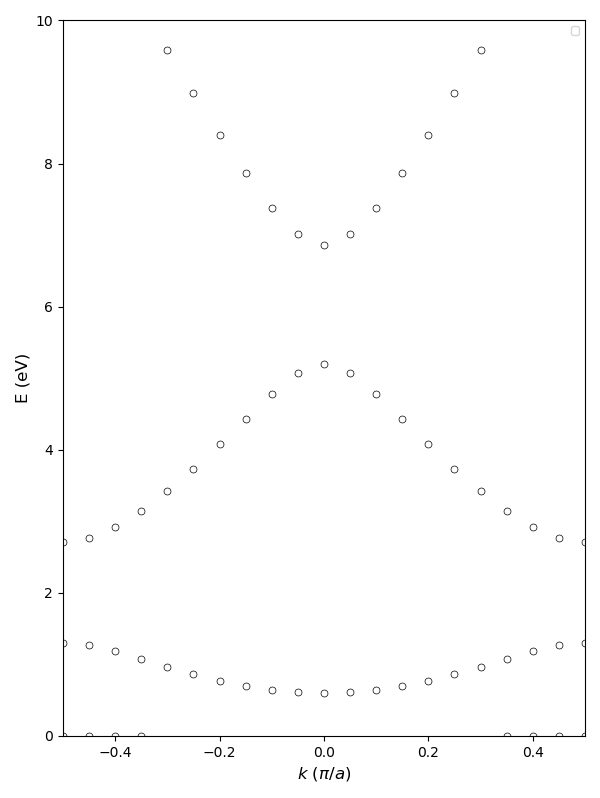
def band():
global mode
global a
global bwidth, bpot
global kmin, kmax, nk
global nEsearch, nMaxLevel
kstep = (kmax - kmin) / (nk - 1)
print("")
print("=== Input parameterss ===")
print("mode:", mode)
print("a=", a, "A")
print("potential: w={} A h={} eV".format(bwidth, bpot))
print("k range: {} - {} at {} step, {} points".format(kmin, kmax, kstep, nk))
print("")
print("")
V0 = bpot
b = bwidth
w = a - b
xk = [kmin + i * kstep for i in range(nk)]
yE = np.zeros([nMaxLevel, nk])
nMaxBand = 0
for ik in range(nk):
k = kmin + ik * kstep
print("at k={:8.4g}".format(k))
Elist, Alist = find_Elist(0.0, V0, nEsearch, k, w, b, V0)
n = len(Elist)
if n > nMaxBand:
nMaxBand = n
for iband in range(min(n, nMaxLevel)):
yE[iband][ik] = Elist[iband]
fig = plt.figure(figsize = figsize)
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_xlim([-0.5, 0.5])
ax1.set_ylim(Erange)
# ax1.set_ylim([0.0, ax1.get_ylim()[1]])
for iL in range(nMaxBand):
ax1.plot(xk, yE[iL], linestyle = '', marker = 'o', markersize = 5.0,
markerfacecolor = 'none', markeredgecolor = 'black', markeredgewidth = 0.5)
ax1.set_xlabel("$k$ $(\pi$$/a)$", fontsize = fontsize)
ax1.set_ylabel("E (eV)", fontsize = fontsize)
ax1.legend(fontsize = legend_fontsize)
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
terminate()
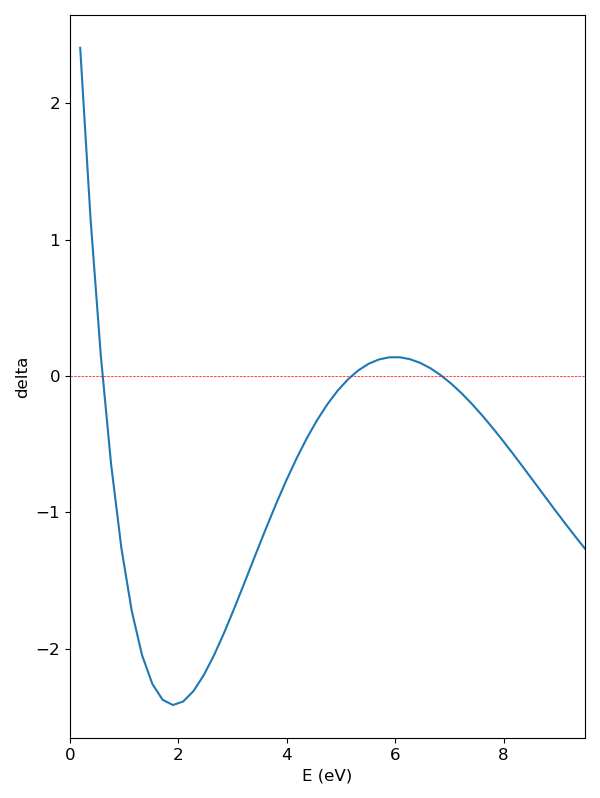
def graphview():
global mode
global a
global bwidth, bpot
global Emin, Emax, nE
Estep = (Emax - Emin) / (nE - 1)
V0 = bpot
b = bwidth
w = a - b
print("")
print("=== Input parameterss ===")
print("mode:", mode)
print("a=", a, "A")
print(" barrier: w={} A h={} eV".format(b, V0))
print(" well : w={} A h={} eV".format(w, 0.0))
print("Energy range: {} - {}, {} eV step {} points".format(Emin, Emax, Estep, nE))
print("at k = {}".format(kg))
print("")
xE = []
yD = []
for i in range(1, nE):
E = Emin + i * Estep
if V0 <= E:
break
delta = cal_delta(E, kg, w, b, V0)
xE.append(E)
yD.append(delta)
fig = plt.figure(figsize = figsize)
ax1 = fig.add_subplot(1, 1, 1)
ax1.plot(xE, yD)
ax1.set_xlim([Emin, Emax])
ax1.plot([Emin, Emax], [0.0, 0.0], linestyle = 'dashed', color = 'r', linewidth = 0.5)
ax1.set_xlabel("E (eV)", fontsize = fontsize)
ax1.set_ylabel("delta", fontsize = fontsize)
# ax1.legend(fontsize = legend_fontsize)
ax1.tick_params(labelsize = fontsize)
plt.tight_layout()
plt.pause(0.1)
print("Press ENTER to exit>>", end = '')
input()
terminate()
def main():
global mode
if mode == 'graph':
graphview()
elif mode == 'band':
band()
elif mode == 'wf':
wf()
else:
terminate("Error: Invalid mode [{}]".format(mode))
if __name__ == "__main__":
main()