No title
Download script from .\slxrd.py
import csv
from pprint import pprint
from math import sin, cos, asin, acos
from cmath import sin as csin, cos as ccos, sqrt as csqrt, exp as cexp
import numpy as np
from matplotlib import pyplot as plt
#=============================
# 定数
#=============================
pi = 3.14159265358979323846
pi2 = pi + pi
pi2i = pi2 * 1j
torad = 0.01745329251944 # rad/deg";
todeg = 57.29577951472 # deg/rad";
#=============================
# 大域変数
#=============================
wl = 1.54 # angstrom
outcsv = 'slxrd.csv'
#=============================
# 構造
#=============================
# 単位格子: c軸長、構造因子、繰り返し数
cells = [
{'a': 4.0, 'F': 10.0, 'N': 5},
{'a': 4.1, 'F': 20.0, 'N': 5},
]
# 層構造: cellsの番号で指定
#layers = [ 0 ]
layers = [ 0, 1 ]
#layers = [ 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1 ]
#layers = [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ]
# 計算する2θ範囲、データ数
range2Q = [5.0, 150.0]
n2Q = 5001
step2Q = (range2Q[1] - range2Q[0]) / (n2Q - 1)
# Complex Laue関数
def cLaue(Q2, N, alatt, wl):
delta = 2.0 * alatt * csin(Q2 / 2.0 * torad) / wl
return (1.0 - cexp(pi2i * delta * N)) / (1.0 - cexp(pi2i * delta))
# diffraction angle theta
def diffQ(d, wl):
sinQ = wl / 2.0 / d
if abs(sinQ) > 1.0:
return None
Q = todeg * asin(sinQ)
return Q
# 構成単位格子の回折角度の計算
print("")
print("Diffraction angles from each unit cell")
for ic in range(len(cells)):
print("cell #{}: a={} F={} N={}"
.format(ic, cells[ic]['a'], cells[ic]['F'], cells[ic]['N']))
for l in range(1, 20):
d00l = cells[ic]['a'] / l
Q_00l = diffQ(d00l, wl)
if Q_00l is None:
break
Q2_00l = 2.0 * Q_00l
if range2Q[0] <= Q2_00l <= range2Q[1]:
sinQ = sin(torad * Q_00l)
LN = sin(pi * cells[ic]['N'] * cells[ic]['a'] * 2.0 * sinQ / wl)
L1 = sin(pi * 1 * cells[ic]['a'] * 2.0 * sinQ / wl)
LN2 = (LN * LN.conjugate()).real
L12 = (L1 * L1.conjugate()).real
I = LN2 / L12
print(" 2Q(00%2d)=%10.6g" % (l, Q2_00l),
" I = %8.4g = %8.4g / %8.4g" % (I, LN2, L12))
# 繰り返し単位格子単位の回折角度の計算
print("")
print("Diffraction angles from each periodic unit cells unit")
for ic in range(len(cells)):
print("unit #{}: a={} F={} N={}"
.format(ic, cells[ic]['a'], cells[ic]['F'], cells[ic]['N']))
for n in range(1, 20):
sinQ = (n + 0.5) * wl / 2.0 / cells[ic]['N'] / cells[ic]['a']
if abs(sinQ) > 1.0:
break
Q2 = 2.0 * todeg * asin(sinQ)
LN = sin(pi * cells[ic]['N'] * cells[ic]['a'] * 2.0 * sinQ / wl)
L1 = sin(pi * 1 * cells[ic]['a'] * 2.0 * sinQ / wl)
LN2 = (LN * LN.conjugate()).real
L12 = (L1 * L1.conjugate()).real
I = LN2 / L12
if range2Q[0] <= Q2 <= range2Q[1]:
print(" 2Q(%2d)=%10.6g" % (n, Q2),
" I = %8.4g = %8.4g / %8.4g" % (I, LN2, L12))
# 回折強度の計算
x = []
y = []
for i in range(n2Q):
Q2 = range2Q[0] + step2Q * i
t = 0.0
F = 0.0
for il in range(len(layers)):
cell = cells[layers[il]]
lf = cLaue(Q2, cell['N'], cell['a'], wl)
delta = 2.0 * t * sin(Q2 / 2.0 * torad) / wl
F += cells[ic]['F'] * lf * cexp(pi2i * delta)
t += cell['a'] * cell['N']
I = (F * F.conjugate()).real
x.append(Q2)
y.append(I)
# print(i, ": ", Q2, lf2)
# CSVファイルへ書き出し
print("")
print("Write to [{}]".format(outcsv))
try:
f = open(outcsv, 'w')
fout = csv.writer(f, lineterminator='\n')
fout.writerow(('2Q', 'Intensity'))
for i in range(0, len(x)):
fout.writerow((x[i], y[i]))
f.close()
except IOError:
print("Error: Can not write to [{}]".format(outfile))
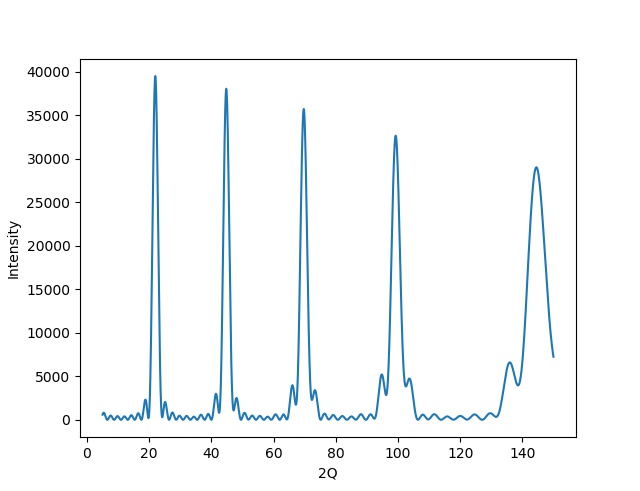
# グラフプロット
plt.plot(x, y, linestyle = 'solid')
plt.xlabel('2Q')
plt.ylabel('Intensity')
plt.pause(0.001)
print("Press ENTER to exit")
input()