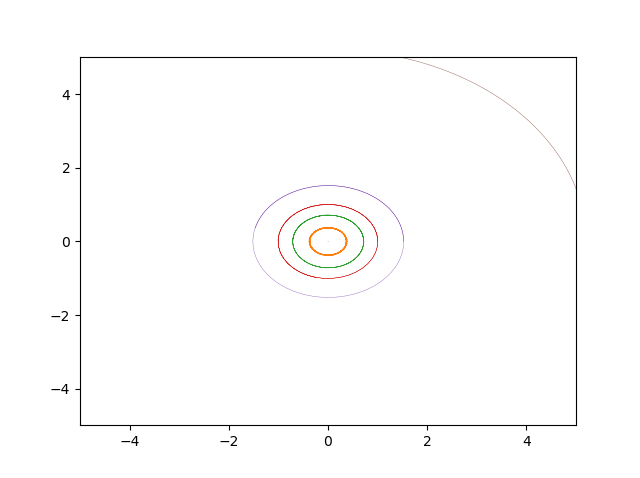
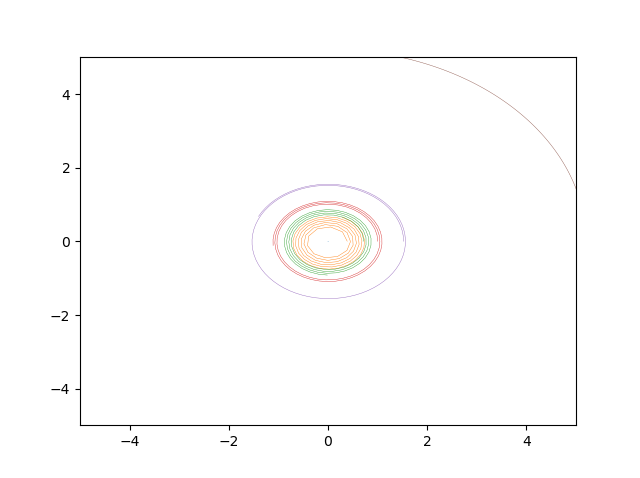
Planet simulator: Solve simulataneous second order diffrential equations
Download script from .\planet.py
import sys
import csv
import numpy as np
from math import exp, sqrt, sin, cos, pi
import matplotlib.pyplot as plt
"""
Planet simulator: Solve simulataneous second order diffrential equations
"""
#===================
# constants
#===================
G = 6.67259e-11 #Nm2/kg2
DayToSecond = 60 * 60 * 24 #s
SecondToDay = 1.0 / DayToSecond
AstronomicalUnit = 1.49597870e11 #m
AU = AstronomicalUnit
G1 = G * DayToSecond * DayToSecond / AU / AU / AU
#===================
# parameters
#===================
# algorism to solve differential equations: 'Euler', 'Verlet'
solver = 'Euler'
#solver = 'Verlet'
fplot = 1 # flag to plot graph: 0: not plot, 1: plot
# planet parameter database
dbfile = 'planet_db.csv'
# trajectries of planets
outfile = "diffeq2nd_Planet_{}.csv".format(solver)
# conservation law of total energy (U) and momenta (Px, Py, Pz)
outfile2 = "diffeq2nd_Planet_{}_conservation.csv".format(solver)
# step time to solve diff eq
dt = 0.1
# maximum steps to be calculated
nt = 20000
# display output control
iprint_interval = 100
nprint_planets = 4
# graph output control
iplotdata_interval = 50
iplot_interval = 500
# graph range
xgrange = (-5.0, 5.0)
ygrange = (-5.0, 5.0)
argv = sys.argv
n = len(argv)
if n >= 2:
solver = argv[1]
if n >= 3:
dt = float(argv[2])
if n >= 4:
nt = int(argv[3])
if n >= 5:
fplot = int(argv[4])
#===================
# functions
#===================
def readdb(dbfile):
planets = []
f = open(dbfile, "r");
reader = csv.DictReader(f)
for row in reader:
planets.append(row)
keys = list(planets[0].keys())
for d in planets:
for key in keys:
if key != 'Name':
d[key] = float(d[key])
return planets
def sum(array):
sum = 0.0
for e in array:
sum += e
return sum
def Ptot(it, M, vx, vy, vz):
Px, Py, Pz = 0.0, 0.0, 0.0
Pmsm = 0.0
np = len(M)
for i in range(0, np):
Pxi = M[i] * vx[i][it];
Pyi = M[i] * vy[i][it];
Pzi = M[i] * vz[i][it];
Px += Pxi
Py += Pyi
Pz += Pzi
Pmsm += Pxi*Pxi + Pyi*Pyi + Pzi*Pzi
Pmsm = sqrt(Pmsm / 3.0 / np)
return Px, Py, Pz, Pmsm
# Normalize total momentum to zero
def normalize_momentum(it, M, x, y, z, vx, vy, vz, fx, fy, fz):
Mtot = sum(M)
Px, Py, Pz, Pmsm = Ptot(it, M, vx, vy, vz);
print("Pinitial = {}, {}, {}".format(Px, Py, Pz))
for ip in range(0, len(M)):
vx[ip][it] -= Px / Mtot;
vy[ip][it] -= Py / Mtot;
vz[ip][it] -= Pz / Mtot;
Px, Py, Pz, Pmsm = Ptot(it, M, vx, vy, vz);
print("Pnormalized = {}, {}, {}".format(Px, Py, Pz))
print("")
return Px, Py, Pz
# set initial normalized positions, velocities, forces
def initialize(planets, M, x, y, z, vx, vy, vz, fx, fy, fz):
global AU
global DayToSecond
for i in range(0, len(planets)):
M.append(planets[i]['Mass'])
x.append([planets[i]['Revolution Radius'] / AU])
y.append([0.0])
z.append([0.0])
vx.append([0.0])
vy.append([planets[i]['Revolution Velocity'] * DayToSecond / AU])
vz.append([0.0])
for i in range(0, len(planets)):
fxi, fyi, fzi = Fi(0, i, M, x, y, z)
fx.append([fxi])
fy.append([fyi])
fz.append([fzi])
# total energy
def Utot(istep, M, x, y, z, vx, vy, vz):
U = 0.0
K = 0.0
for i in range(0, len(M)):
K += 0.5 * M[i] \
* (vx[i][istep]*vx[i][istep] + vy[i][istep]*vy[i][istep] + vz[i][istep]*vz[i][istep])
for j in range(i+1, len(M)):
dx = x[j][istep] - x[i][istep]
dy = y[j][istep] - y[i][istep]
dz = z[j][istep] - z[i][istep]
r2 = dx*dx + dy*dy + dz*dz
r = sqrt(r2)
U += G1 * M[i] * M[j] / r
return U, K, U + K
# i - j interplanet normalized force devided by i-th planets mass
def Fij(istep, i, j, M, x, y, z):
dx = x[j][istep] - x[i][istep]
dy = y[j][istep] - y[i][istep]
dz = z[j][istep] - z[i][istep]
r2 = dx*dx + dy*dy + dz*dz
r = sqrt(r2)
g = G1 * M[j]
f = g / r2
fx = f * dx / r
fy = f * dy / r
fz = f * dz / r
return fx, fy, fz
# normalized force on i-th planet devided by its mass
def Fi(istep, i, M, x, y, z):
fxi = 0.0
fyi = 0.0
fzi = 0.0
for j in range(0, len(M)):
if i == j:
continue
fxj, fyj, fzj = Fij(istep, i, j, M, x, y, z)
fxi += fxj
fyi += fyj
fzi += fzj
# print("f={}, {}, {}".format(fxi, fyi, fzi))
return fxi, fyi, fzi
#===================
# main routine
#===================
def main():
global plt
global nt
global dt
print("Planet simulator: Solve simulataneous second order diffrential equations by Euler method")
print("G = {} Nm2/kg2".format(G))
print("AU = {:e} m".format(AU))
print("G1 = {}".format(G1))
print("")
# read planet database
print("Planets:")
planets = readdb(dbfile)
keys = list(planets[0].keys())
for d in planets:
print(" ", d['Name'])
for key in keys:
if key != 'Name':
print(" {}: {}".format(key, d[key]))
print("")
# create list variables and normalize
M = []
x = []
y = []
z = []
xg = []
yg = []
zg = []
vx = []
vy = []
vz = []
fx = []
fy = []
fz = []
initialize(planets, M, x, y, z, vx, vy, vz, fx, fy, fz)
Px, Py, Pz = normalize_momentum(0, M, x, y, z, vx, vy, vz, fx, fy, fz)
print("")
# make label list for display / csv output
labellist = ['t']
for i in range(0, len(planets)):
labellist.append("x({})".format(planets[i]['Name']))
labellist.append("y({})".format(planets[i]['Name']))
# open outfile to write a csv files
print("Write to [{}]".format(outfile))
f = open(outfile, 'w')
fout = csv.writer(f, lineterminator='\n')
fout.writerow(labellist)
f2 = open(outfile2, 'w')
fout2 = csv.writer(f2, lineterminator='\n')
fout2.writerow(['t', 'U', 'K', 'E', 'Px', 'Py', 'Pz', 'Pmsm'])
print("{:^5}".format('t'), end = '')
for i in range(1, nprint_planets*2, 2):
print(" {:^12} {:^12}".format(labellist[i], labellist[i+1]), end = '')
print("")
# create figure object and axes list
if fplot == 1:
fig, ax = plt.subplots(1, 1)
plots = []
# Solve the 1st data by Euler or Heun method
datalist = [0.0]
print("{:^5}".format(0.0), end = '')
for i in range(0, len(planets)):
fx0, fy0, fz0 = Fi(0, i, M, x, y, z)
vx1 = vx[i][0] + dt * fx0
vy1 = vy[i][0] + dt * fy0
vz1 = vz[i][0] + dt * fz0
x1 = x[i][0] + dt * vx[i][0]
y1 = y[i][0] + dt * vy[i][0]
z1 = z[i][0] + dt * vz[i][0]
datalist.append(x[i][0])
datalist.append(y[i][0])
x[i].append(x1)
y[i].append(y1)
z[i].append(z1)
vx[i].append(vx1)
vy[i].append(vy1)
vz[i].append(vz1)
if fplot == 1:
xg.append([x1])
yg.append([y1])
zg.append([z1])
lines, = ax.plot(x[i], y[i], linewidth = 0.3)
plots.append(lines)
for i in range(1, nprint_planets*2, 2):
print(" {:>12.4f} {:>12.4f}".format(x[i][0], y[i][0]), end = '')
print("")
fout.writerow(datalist)
U, K, E = Utot(0, M, x, y, z, vx, vy, vz)
Px, Py, Pz, Pmsm = Ptot(0, M, vx, vy, vz)
fout2.writerow([0.0, U, K, E, Px, Py, Pz, Pmsm])
# Solve the 2nd and later steps
for it in range(1, nt+1):
t = it * dt
# print("it={} t={}".format(it, t))
datalist = [t]
if it % iprint_interval == 0:
print("{:^5}".format(t), end = '')
xmin = 0.0
xmax = 0.0
ymin = 0.0
ymax = 0.0
for i in range(0, len(planets)):
fx0, fy0, fz0 = Fi(it, i, M, x, y, z)
if solver == 'Euler':
vx1 = vx[i][it] + dt * fx0
vy1 = vy[i][it] + dt * fy0
vz1 = vz[i][it] + dt * fz0
x1 = x[i][it] + dt * vx[i][it]
y1 = y[i][it] + dt * vy[i][it]
z1 = z[i][it] + dt * vz[i][it]
elif solver == 'Verlet':
x1 = 2.0 * x[i][it] - x[i][it-1] + dt*dt * fx0
y1 = 2.0 * y[i][it] - y[i][it-1] + dt*dt * fy0
z1 = 2.0 * z[i][it] - z[i][it-1] + dt*dt * fz0
vx1 = (x1 - x[i][it-1]) / 2.0 / dt
vy1 = (y1 - y[i][it-1]) / 2.0 / dt
vz1 = (z1 - z[i][it-1]) / 2.0 / dt
datalist.append(x[i][it])
datalist.append(y[i][it])
x[i].append(x1)
y[i].append(y1)
z[i].append(z1)
vx[i].append(vx1)
vy[i].append(vy1)
vz[i].append(vz1)
if fplot and (it % iplotdata_interval == 0):
xg[i].append(x1)
yg[i].append(y1)
zg[i].append(z1)
# add trajectry data (x[i], y[i]) to the axes object plaots[i]
# get x- and y-ranges to be displayed in the graph
if fplot and i <= 6:
plots[i].set_data(xg[i], yg[i])
xmin = min([xmin] + x[i])
xmax = max([xmax] + x[i])
ymin = min([ymin] + y[i])
ymax = max([ymax] + y[i])
# display output every iprint_interval steps
if it % iprint_interval == 0:
for i in range(1, nprint_planets*2, 2):
print(" {:>12.4g} {:>12.4g}".format(x[i][it], y[i][it]), end = '')
print("")
# write to trajectory csv file
fout.writerow(datalist)
# write to conservation csv file
U, K, E = Utot(it, M, x, y, z, vx, vy, vz)
Px, Py, Pz, Pmsm = Ptot(it, M, vx, vy, vz)
fout2.writerow([t, U, K, E, Px, Py, Pz, Pmsm])
# update the graph every iplot_interval steps
if fplot and it % iplot_interval == 0:
ax.set_xlim(xgrange)
ax.set_ylim(ygrange)
# ax.set_xlim((xmin, xmax))
# ax.set_ylim((ymin, ymax))
plt.pause(1.e-10)
f.close()
print("Press ENTER to exit>>", end = '')
input()
exit()
if __name__ == '__main__':
main()